|
Introduction On the surface, the teaching of quantum mechanics seems like a specialized topic for those teaching physics. In fact, because of its fundamental role in physics and chemistry, quantum mechanics is one of the most widely taught topics on the college and university level. Undergraduates encounter quantum mechanics in their introductory physics, modern physics, physical chemistry, statistical and thermal physics, and quantum mechanics courses, while graduate students may take as many as five additional courses in quantum mechanics and quantum field theory. Despite the importance of quantum theory, the teaching of quantum mechanics in chemistry and physics has not changed significantly since quantum mechanics was invented. In addition, studies have shown that there is very little difference between an undergraduate’s conceptual understanding of quantum mechanics and a graduate student’s conceptual understanding of quantum mechanics [1]. Recent advances in computational power, however, have made many heretofore inaccessible topics in theoretical and computational quantum mechanics more accessible to teachers and their students. We have created many exercises for studying energy eigenstates (so-called stationary states) which have been reported elsewhere [2,3]. This paper describes the technology and pedagogy of a suite of Java programs that explore the dynamics of quantum-mechanical wave packets in an infinite square well. By now it is hard to imagine a teacher who has not heard the call to ‘teach with technology’ as it has resounded through educational institutions and government agencies alike. However, teaching with technology, just for the sake of teaching with technology, has often resulted in the development and use of tools that are not pedagogically sound [4,5]. Into this environment, we introduced Physlets®, a collection of interactive computer simulations [6] and accompanying curricular materials [7-11] designed with a sound use of pedagogy in mind [12-15]. The aim of Physlets is to provide a resource for teaching that enhances student learning through interactive engagement [16-18]. At the same time, Physlets are flexible enough (all Physlets can be set up and controlled with JavaScript) to be adapted to a variety of pedagogical strategies and local environments. Physlets are free for noncommercial use and are based on HTML and open internet standards (Physlets run on any platform: Macintosh OSX Panther, Windows, and Linux, with Java-enabled browsers that support Java-to-JavaScript communication such as: Safari, Internet Explorer, or Mozilla). Physlet-based curricular material is easy to translate into other languages and Physlet Web sites can be found throughout the world [19]. While we have focused on topics from physics, such as quantum mechanics, Physlets can be used to create exercises for many other fields such as mathematics, chemistry [11], biology, and economics [2].
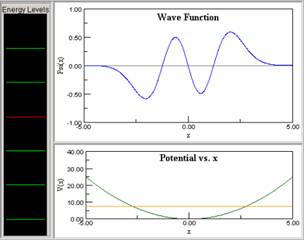
The Physlet paradigm, an example of which is shown in Figure 1, is based on the Model-View-Control (MVC) design pattern which is one of the most successful software architectures ever invented. The model maintains data and provides methods by which that data can change; the control gives the user the ability to interact with the model using the keyboard and the mouse; and the view presents a visual representation of the model’s data. Java is ideal for the implementation of models and views because these objects are often complex and computational speed is important. But since the control object is accessed infrequently and should be customizable, it can be implemented differently. A scripting language such as JavaScript embedded into an HTML document provides an ideal solution. The advantage of using JavaScript and HTML to control a model and its views is that a common user interface can be created to ease the learning curve across pedagogical contexts. This unique approach has contributed to the success and wide adoption of Physlets. For example, a Google search on “Physlets” returns over 12,000 Web pages. Open Source Physics While Physlets are in many ways ‘open,’ they are not open source. As a consequence, the underlying Java code is inaccessible. This approach works for general-purpose applications, but fails for more sophisticated one-of-a-kind simulations that require advanced discipline-specific expertise, such as those for quantum mechanics. Users and developers of these types of programs often have specialized curricular needs that can only be addressed by having access to the source code. However, anyone who has ever written a program in Java knows that writing code for creating buttons, text fields, and graphs can be tedious and time consuming. The Open Source Physics (OSP) project [20] solves this problem by providing a consistent object-oriented library of Java components (OSP libraries are based on Swing and Java 1.4) for anyone wishing to write their own programs.
Open Source Physics curricular material is written in Java and distributed using internet technologies. Although we distribute source code under the GNU GPL license, the modification and redistribution of compiled Java programs is not an easy task for many teachers and students. It is not, however, necessary to become expert in programming to use our materials. Although the source code will be available for Java experts, our programs store their internal parameters using Extensible Markup Language (XML). A teacher can, for example, load a pre-defined multi-state quantum superposition demonstration using the data saved as an XML file shown in Figure 3. Because XML data files are character-based, it is straightforward to edit properties such as the expansion coefficients to create custom simulations.
Like Physlets, OSP provides a framework for embedding programs into HTML pages and for controlling these programs using JavaScript. Unlike Physlets, programs can also be run as Java applications. The Launcher program shown in Figure 4 enables authors to distribute collections of OSP programs and curricular material in consistent self-contained packages.
Launcher is designed to execute multiple Java applications or multiple copies of a single Java application with different initial conditions. Launcher also uses an XML file to store its properties, as shown in Figure 5.
Java-based curricular material has traditionally been distributed over the Internet using applets. Sun Microsystems has recently released a new technology known as Java Web Start that combines the applet and application approaches. Java Web Start is a helper application that is associated with a Web browser. When a user clicks on a link within an HTML page that points to a special file on the server, it causes the browser to launch Java Web Start, which then automatically downloads, caches, and runs the Java-based application. The entire process is typically completed without requiring any user interaction, except for the initial single click. A number of Java Web Start Launcher packages can be downloaded and run from the OSP Web site. Quantum-mechanical Wave Packets Wave Packet Revivals: Visualization Time-dependent quantum-mechanical wave functions are inherently complex (having real and imaginary components) due to the time evolution governed by the Schrödinger equation. The standard way to visualize the wave function considers the probability density in position or momentum space (more typically position space), an approach that discards all phase information.
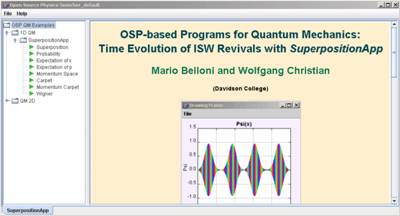
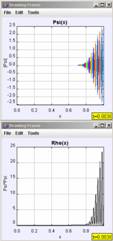
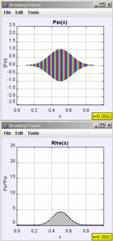
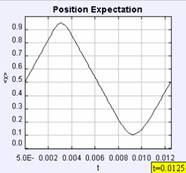
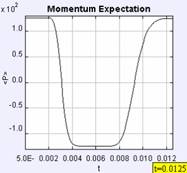
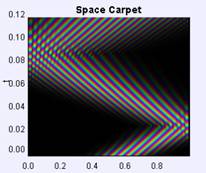
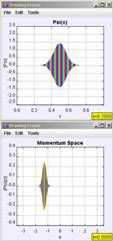
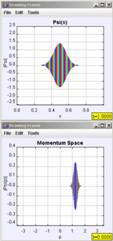
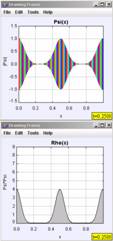
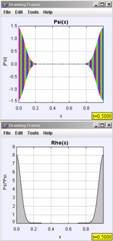
Figure 6 shows the short-term time evolution of the probability density of a Gaussian wave packet in an infinite well with walls at x = 0 and x = 1. The packet has an initial momentum to the right and the images are shown at equal-time intervals. We are supposed to imagine the motion of the packet by reading the images from left to right. We notice that as the packet moves to the right its leading edge encounters the infinite wall first and reflects to the left back towards the middle of the well. There are several interesting features about this problem that are not depicted in the image, however. While we get the general sense of what happens, we lose a lot of the specific details by focusing on just one facet of the motion. This is especially apparent at the collision with the wall. At the classical collision time, the classical momentum is zero, yet in the quantum-mechanical case, the average momentum of the packet is negative [21,22]. On the much longer revival time scale we are interested in visualizing the fractional and exact quantum-mechanical revivals of the initial wave packet. One can again look at the position-space probability density, but there is no guarantee that by just looking we can recognize precisely when the revivals occur. In addition, showing just one image lacks the ability to show how the change of initial conditions affects the resulting dynamics. Well-crafted computer simulations, however, can. The following OSP examples show the time evolution of wave packet dynamics in the infinite square well. We focus on the quantum ‘bounce’ and quantum-mechanical revivals and use the time dependence of the expectation values [23], so-called quantum carpets [24] and, in the future, the joint position-momentum quasi-probability density using the Wigner function [25] to uniquely depict wave packet evolution in time. A brief tutorial on wave packet phenomena and quantum-mechanical revivals [26-28] can be found in the Appendix.
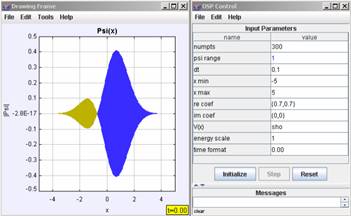
For our initial Gaussian wave packets we use a variety of initial momentum values corresponding to the central values of n0 = 0, 10, 20, 40, and 80 (where p0 = n0π/L), so that the ratio of classical periodicity to spreading time varies (for n0 = 40, Tcl/t0 = 10/π, and significant spreading can be seen even over half a classical period). For ease of calculation, we also set 2m = L = h = 1, while allowing the user to vary x0, p0, and Δx0 = b/√2. Using our simplifications, the revival time, Trev, becomes: Trev = 2n0Tcl = 2/π. For the infinite square well, longer time scales are not present due to the purely quadratic dependence of the energy eigenvalues. The revival time scale can clearly be much larger than the classical period for wave packets characterized by n0>>1 (giving Trev/Tcl = 2n0, which for n0 = 40 gives Trev/Tcl = 80). The program we use to study revivals, QMSuperposition, inputs the expansion coefficients, cn, of a general quantum-mechanical superposition shown in Eq. (A2). The program does so by separately inputting the real, Re[cn], and imaginary, Im[cn] parts of the expansion coefficients, cn (which were separately calculated in Mathematica). An XML file, such as the one shown in Figure 3, stores these expansion coefficients and other appropriate initial conditions for the program. The wave functions are then calculated either numerically for any user-defined potentiaon QMSuperpositionApp (which itself only shows the wave function) can be chosen:
The use of analytic solutions for each eigenstate allows the simulation to run for a long period of time and yet never accumulate numerical error since the wave function is calculated anew at each time step. In addition, within the OSP control, we can set the energy scale, which determines the time scale for the animation. For example, setting the energy scale to 2/π forces Trev = 1, which is a convenient time scale for the study of revivals and fractional revivals which occur at Trev and fractions of Trev, respectively. The applications described here can be organized using Launcher. Once Launcher is opened, the user can double click on a node to run a program with the initial conditions stored in the associated XML file.
Evolution of a Quantum Wave Packet: Short- and Long-term Behavior in the Infinite Well
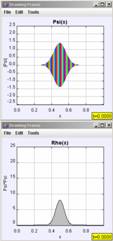
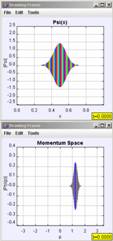
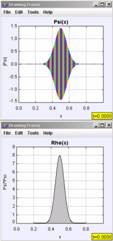
In the following examples we will focus on the time evolution of Gaussian wave packets in the infinite square well. In time-dependent quantum mechanics it is necessary to describe the wave function in terms of complex (real and imaginary) functions. In order to animate these time-dependent functions, we use an amplitude and phase representation of the wave function. The amplitude is drawn centered on the y-axis and is the height of the envelope shown from top to bottom. The phase, or phase angle, of the wave function is shown as color and we often show a color-conversion image, as in Figure 8 to help students determine the phase of the wave function.
Time Evolution of a Quantum Wave Packet on a Ring
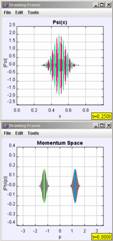
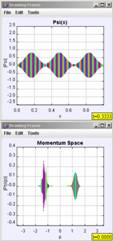
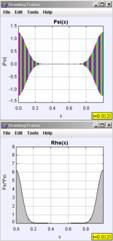
The final example we will discuss is that of a Gaussian wave packet confined on a circular ring using the program QMSuperpositionProbabilityApp and the potential energy function, V(x) set equal to “ring.” This is the same program used in Figure 9, but now it uses periodic boundary condition. Here we visualize this example in two-dimensions, but elsewhere we have used the new Open Source Physics Java3D library [3,20] to show a three-dimensional depiction of the wave packet’s evolution. As shown in Figure 12, the Gaussian wave packet evolves over time and undergoes quantum-mechanical revivals. For this system, the wave packet again has an average momentum, causing it to move around the ring, and again it spreads. After a short time, the spreading is large enough that the front of the wave packet starts to interfere with the back of the wave packet. At fractions of Trev, the revival time, the wave packet, or ‘mini-packet clones’ of the original wave packet, can form. Conclusion We have created over 150 Physlet- and Open Source Physics-based exercises for the teaching and learning of quantum mechanics. Some of these exercises can be found on the Web site in Ref. [2]. Most of the new exercises, such as the ones presented in this paper, can be found on the Open Source Physics Web site (http://www.opensourcephysics.org) and on the MERLOT (https://merlot.org) and ComPADRE (http://compadre.org/quantum) digital libraries by searching for “Physlets” or “Open Source Physics.” These materials provide a new, exciting, and effective way to deliver interactive curricular material to students studying quantum mechanics. The effectiveness of these materials is supported by our preliminary assessment of the use of interactive curricular material in our quantum mechanics courses [2]. We are currently developing additional material that will appear in the book: Physlet Quantum Mechanics (2005 Prentice Hall). Acknowledgements
Appendix Wave Packet Revivals: Theory Quantum-mechanical wave packet revivals have recently received considerable theoretical and experimental attention (Robinett, 2004). Most often the theoretical research has focused on initially localized wave packets in the infinite square well (ISW) because of its well-known time scales: the classical time scale and the revival time scale. We examine the time dependence of such an initially localized state by choosing a standard Gaussian wave packet of the form
where by direct calculation: <x>t = 0 = x0, <p>t = 0 = p0, and Δxt = 0 = Δx0 = b/√2. The wave packet can be constructed from a sum of energy eigenstates as:
where the expansion coefficients satisfy Σn |cn|2 = 1. The expansion coefficients are determined by an ‘overlap’ integral of the individual energy eigenstates with the initial Gaussian wave packet. We find that over time the wave packet spreads in a characteristic way defined by the spreading time, t0 = mb2/h. For longer times, we have the so-called classical period, Tcl, and the revival time, Trev, which are related to each other by:
The classical periodicity for the ISW agrees with the classically-expected result (Tcl = 2L/v which corresponds to the time it takes a classical particle to traverse the well twice). The so-called initial ‘bounce’ at Tcl/4 with one wall is of interest because of the similarities and differences between the classical and quantum-mechanical cases (Andrews, 1998, Doncheski & Robinett, 2004). Also of interest in the context of the ISW, but on a considerably longer time scale than the classical time scale, are the well-known exact, mirror, and fractional revivals (Averbukh & Perleman, 1989, Bluhm, Kostelecky, & Porter, 1996, Aronstein & Stroud, 1997) in which the wave packet or copies (sometimes called ‘mini-packets’ or ‘clones’) of the original wave packet reform long after the original packet ‘collapses.’ The analysis of these problems often requires specialized visualization techniques because of the long times involved. References [1] E. Cataloglu and R. Robinett, “Testing the Development of Student Conceptual and Visualization Understanding in Quantum Mechanics through the Undergraduate Career,” American Journal of Physics, 70, 238-251 (2002). [2] M. Belloni and W. Christian, “Physlets for Quantum Mechanics,” Computing in Science and Engineering 5, 90 (2003). The Physlet-based quantum mechanics exercises from this paper are available at: http://webphysics.davidson.edu/cise_qm. [3] M. Belloni, L. Cain, and W. Christian, “Using Physlets and Open Source Physics to Make Quantum Mechanics Visual and Interactive,” Transformations: Liberal Arts in the Digital Age Volume 2, No. 1 (2004). [4] A. Szabo and N. Hastings, Using IT in the undergraduate classroom: should we replace the blackboard with PowerPoint?, Computers and Education 35, 175-187, 2000. [5] R. Beichner, “The Impact of Video Motion Analysis on Kinematics Graph Interpretation Skills,” American Journal of Physics, 64, 1272-1277 (1997). [6] W. Christian and M. Belloni, Physlets: Teaching Physics with Interactive Curricular Material, Prentice Hall, Upper Saddle River, NJ, 2001. See also: http://webphysics.davidson.edu/applets/applets.html. [7] M. H. Dancy, W. Christian, and M. Belloni, “Teaching with Physlets®: Examples From Optics,” The Physics Teacher, 40, 40-45 (2002). [8] A. J. Cox, M. Belloni, W. Christian, and M. H. Dancy, “Teaching Thermodynamics with Physlets® in Introductory Physics,” Physics Education, 38, 433-440 (2003). [9] W. Christian and M. Belloni, Physlet® Physics: Interactive Illustrations, Explorations, and Problems for Introductory Physics, Prentice Hall, Upper Saddle River, NJ, 2004. [10] M. Belloni, W. Christian, and Melissa Dancy, “Teaching Special Relativity Using Physlets,” The Physics Teacher, 42, 284-290 (2004). [11] D. N. Blauch, “Java Classes for Managing Chemical Information and Solving Generalized Equilibrium Problems,” Journal of Chemical Information and Computer Science, 42, 143-146 (2002). [12] G. Novak, E. Patterson, A. Gavrin, and W. Christian, Just-in-Time Teaching: Blending Active Learning with Web Technology, Prentice Hall, Upper Saddle River, NJ, 1999. [13] E. Mazur, Peer Instruction: A Users Manual, Prentice Hall, Upper Saddle River, NJ, 1997. [14] T. O’Kuma, D. Maloney, and C. Hieggelke, Ranking Task Exercises in Physics, Prentice Hall, Upper Saddle River, NJ, 2000. [15] L. McDermott and P. Schaffer and the Physics Education Group, Tutorials in Introductory Physics, Prentice Hall, Upper Saddle River, NJ, 2001. [16] R. Hake, “Interactive-engagement vs. Traditional Methods: A Six-thousand-student Survey of Mechanics Test Data for Introductory Physics,” American Journal of Physics, 66, 64 (1998). [17] D. Sokoloff and R. Thornton, “Using Interactive Lecture Demonstrations to Create an Active Learning Environment,” The Physics Teacher, 35, 340 (1997). [18] B. Thacker, “Comparing Problem Solving Performance of Physics Students in Inquiry-based and Traditional Introductory Courses,” American Journal of Physics, 62, 627 (1994). [19] Francisco Esquembre, Ernesto Martín, Wolfgang Christian y Mario Belloni, Fislets: Enseñanza de la Física con Material Interactivo, Prentice-Hall, España, 2004. [20] The Open Source Physics code library, documentation, and curricular material can be downloaded from the Web site: http://www.opensourcephysics.org/default.html. [21] M. Andrews, “Wave packets bouncing off walls,” Am. J. Phys., 66, 252-254 (1998). [22] M. A. Doncheski and R. W. Robinett, “Anatomy of a quantum ‘bounce’,” European Journal of Physics, 20, 29-37 (1999). M. Belloni, M. A. Doncheski and R. W. Robinett, “Exact Results for Gaussian ‘Bouncing’ Wave Packets,” accepted to Physica Scripta (2004). [23] R. W. Robinett, “Visualizing the Collapse and Revival of Wave Packets in the Infinite Square Well Using Expectation Values,” Am. J. Phys, 68, 410-42 (2000). [24] F. Grossmann, J.-M. Rost, and W. P. Schleich, “Spacetime Structures in Simple Quantum Systems,” J. Phys., A30, L277-L283 (1997); W. Loinaz and T. J. Newman, “Quantum Revivals and Carpets in Some Exactly Solvable Systems,” J. Phys. A: Math. Gen., 32, 8889-8895 (1999). [25] M. Belloni, M. A. Doncheski and R. W. Robinett, “Wigner Quasi-probability Distribution for the Infinite Square Well: Energy Eigenstates and Time-dependent Wave Packets,” American Journal of Physics., 74, 1183-1192 (2004). [26] I. Sh. Averbukh and N. F. Perelman, “Fractional Revivals: Universality in the Long-term Evolution of Quantum Wave Packets Beyond the Correspondence Principle Dynamics,” Phys. Lett., A139, 449-453 (1989); “Fractional Revivals of Wave Packets,” Acta Phys. Pol., 78, 33-40 (1990). [27] R. Bluhm, V. A. Kostelecky, and J. Porter, “The Evolution and Revival Structure of Localized Quantum Wave Packets,” Am. J. Phys., 64, 944-953 (1996). [28] D. L. Aronstein and C. R. Stroud, Jr., “Fractional Wave-function Revivals in the Infinite Square Well,” Phys. Rev., A55, 4526-4537 (1997). [29] For an extensive review of this topic see: R. W. Robinett, “Quantum Wave Packet Revivals,” Physics Reports, 392 1-119 (2004). ReferencesAndrews, M. (1998). Wave packets bouncing off walls,” Am. J. Phys., 66, 252-254. Aronstein, D. L. & Stroud, C. R. Jr. (1997) Wave-function Revivals in the Infinite Square Well,” Phys. Rev., A55, 4526-4537. Averbukh, I. S. & Perelman, N. F. (1989). Fractional Revivals: Universality in the Long-term Evolution of Quantum Wave Packets Beyond the Correspondence Principle Dynamics,” Phys. Lett., A139, 449-453. “Fractional Revivals of Wave Packets,” Acta Phys. Pol., 78, 33-40 (1990). Beichner, R. (1997). The Impact of Video Motion Analysis on Kinematics Graph Interpretation Skills. American Journal of Physics, 64, 1272-1277. Belloni, M. and W. Christian, W. (2003). Physlets for Quantum Mechanics. Computing in Science and Engineering, 5, 90. (The Physlet-based quantum mechanics exercises from this paper are available at: http://webphysics.davidson.edu/cise_qm.) Belloni, M., L. Cain, L. & Christian, W. (2004). Using Physlets and Open Source Physics to Make Quantum Mechanics Visual and Interactive,” Transformations: Liberal Arts in the Digital Age, 2, No. 1. Belloni, M., Christian, W. & Dancy, M. (2004) Teaching Special Relativity Using Physlets. The Physics Teacher, 42, 284-290. Belloni, M., Doncheski, M. A., & Robinett, R. W. (2004). Wigner Quasi-probability Distribution for the Infinite Square Well: Energy Eigenstates and Time-dependent Wave Packets,” American Journal of Physics., 74, 1183-1192. Blauch, D. N. (2002). Java Classes for Managing Chemical Information and Solving Generalized Equilibrium Problems. Journal of Chemical Information and Computer Science, 42, 143-146 (2002). Bluhm, R. Kostelecky, V. A. & Porter, J. (1996), The Evolution and Revival Structure of Localized Quantum Wave Packets. Am. J. Phys., 64, 944-953. Cataloglu, E. & Robinett, R. (2002). Testing the Development of Student Conceptual and Visualization Understanding in Quantum Mechanics through the Undergraduate Career. American Journal of Physics, 70, 238-251. Christian, W. & M. Belloni, M. (2001). Physlets: Teaching Physics with Interactive Curricular Material, Prentice Hall, Upper Saddle River, NJ. (See also: http://webphysics.davidson.edu/applets/applets.html) Christian, W. & Belloni, M. (2004). Physlet® Physics: Interactive Illustrations, Explorations, and Problems for Introductory Physics, Prentice Hall, Upper Saddle River, NJ. Cox, A. J., Belloni, M., Christian, W. & Dancy, M. H. (2003). Teaching Thermodynamics with Physlets® in Introductory Physics. Physics Education, 38, 433-440. Doncheski, M. A. & Robinett, R. W. (2004). Anatomy of a quantum ‘bounce’,” European Journal of Physics, 20, 29-37 (1999).&nbp; M. Belloni, M. A. Doncheski and R. W. Robinett, “Exact Results for Gaussian ‘Bouncing’ Wave Packets,” accepted to Physica Scripta. Esquembre, F., Martín, E., Christian, W. y Belloni, M. (2004) Fislets: Enseñanza de la Física con Material Interactivo, Prentice-Hall, España. Grossmann, F., Rost, J. M. & Schleich, W. P. (1997). Spacetime Structures in Simple Quantum Systems,” J. Phys., A30, L277-L283. Hake, R. (1998). Interactive-engagement vs. Traditional Methods: A Six-thousand-student Survey of Mechanics Test Data for Introductory Physics. American Journal of Physics, 66, 64. Loinaz, W. & T. J. Newman, T. J. (1999). Quantum Revivals and Carpets in Some Exactly Solvable Systems,” J. Phys. A: Math. Gen., 32, 8889-8895. Mazur, E. (1997). Peer Instruction: A Users Manual, Prentice Hall, Upper Saddle River, NJ. McDermott, L., Schaffer, P., & the Physics Education Group. (2001). Tutorials in Introductory Physics, Prentice Hall, Upper Saddle River, NJ. Novak, G., Patterson, E., Gavrin, A. & Christian, W. (1999). Just-in-Time Teaching: Blending Active Learning with Web Technology, Prentice Hall, Upper Saddle River, NJ. O’Kuma, T., Maloney, D. & Hieggelke, C. (2000). Ranking Task Exercises in Physics, Prentice Hall, Upper Saddle River, NJ. Robinett, R. W. (2000). Visualizing the Collapse and Revival of Wave Packets in the Infinite Square Well Using Expectation Values. Am. J. Phys, 68, 410-42. Robinett, R.W. (2004). Quantum Wave Packet Revivals,” Physics Reports, 392, 1-119. Sokoloff, D. & Thornton, R. (1997) Using Interactive Lecture Demonstrations to Create an Active Learning Environment. The Physics Teacher, 35, 340. Szabo, A. & Hastings, N. (2000) Using IT in the undergraduate classroom: should we replace the blackboard with PowerPoint?, Computers and Education, 35, 175-187. Thacker, B. (1994). Comparing Problem Solving Performance of Physics Students in Inquiry-based and Traditional Introductory Courses. American Journal of Physics, 62, 627.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Copyright © 2005 MERLOT. All Rights Reserved. Portions Copyright by MERLOT Community Members. Used with Permission. |
Questions? Email: jolteditor@merlot.org Last Modified : 2005/04/14 |