Introduction

Mathematics has become the gateway to careers in many fields, ranging from the sciences to economics, commerce and other social sciences. Increasing use of sophisticated statistical analysis and modelling in non-science domains compels students to enrol and succeed in college level mathematics courses (e.g., Calculus). Nevertheless, the enrolment in introductory college level mathematics courses is declining. Mathematical knowledge and numeracy of students in North America is ebbing, whether in comparison to students who graduated in the past or to students living in other OECD (Organisation for Economic Cooperation and Development) countries (e.g., National Centre for Education Statistics, 2006; Statistics Canada and OECD, 2005). The failure rate in mathematics courses taken by non-science students hovers around 50% (e.g., Gordon, 2005). This study aimed to determine whether student achievement in Calculus courses could be improved, reversing the current trends. To this end, three instructional settings in Calculus classes, two of which integrate available Web-based technology, were developed on the basis of current knowledge concerning the teaching of mathematics, and then the effectiveness of these designs was evaluated experimentally. The outcomes of this experiment, in terms of students’ academic performance (knowledge of Calculus) and motivation, as well as the implications of this research are reported below.

Theoretical Perspective

To stem the decline in success rates in Calculus, numerous reforms of mathematics education, many of them rooted in the constructivist paradigm of learning and teaching, e.g., Calculus Reform Movement (Hodgson, 1987), have been developed over the past few decades. However, the decline in mathematical knowledge, enrolment and success rates persists. Some researchers (e.g., Ball and Farzani, 2007) attribute the failures of reforms to faults in their implementation. The fact is that reformers’ recommendations have not been adopted by many instructors (Handelsman, Ebert-May, Beichner, Bruns, Chag, DeHaan, Gentile, Lauffer, Stewart,Tilghman and Wood, 2004). One of the reasons why instructors are wary of reforms may be that mathematics instructors question reformers’ premise that the current trends are caused by teaching “rigorous” mathematics (Klein and Rosen, 1997). In addition, while reformers recommend teaching mathematics through discovery, cognitive psychologists question the wisdom of such approaches and suggest that direct instruction is more likely to promote construction of knowledge (Meyer, 2004; Kirschner, Sweller and Clark, 2006). In summary, radical reforms of what we teach and how we teach mathematics appear to be an unlikely remedy to the current trends, and only some of the reformers’ recommendations were adopted in this experiment. The instructors in this experiment used the direct-instruction approach but emphasized graphical, numerical and verbal perspectives of concepts as reformers have recommended.

With the advent of graphing calculators, computers and the Web, enthusiastic mathematics instructors have developed a host of instructional strategies and tools (e.g., simulations) attempting to integrate these technologies into teaching mathematics. At the same time, researchers have been intensively studying the effectiveness of these strategies (variously labelled computer-assisted instruction (CAI), e-learning, integration of technology (IT), etc.) over the past decades, and most will agree that “the jury is still out” on whether the integration of technology in the classroom really improves instruction in contrast to the traditional “chalk and board”. There are numerous reasons for this lack of definitive answers. Some of them are methodological: for example, Bernard, Abrami and Wade (2007), in their metanalysis of Canadian studies, have included 762 studies but only 2.2% of those studies were experimental or quasi-experimental quantitative studies. This seems to indicate that only a small number of studies are designed to provide empirical evidence of superior achievement when technology is integrated into the instructional design. Bernard et al. (2007) report a small positive mean effect size (0.117) which is not much different from the mean effect size 0.127 reported by an earlier meta-analysis (Christmann and Badgett, 2000). In contrast, Kulik (2003) compared the results of 12 quasi-experimental studies involving use of graphing calculators and/or computer algebra systems in mathematics courses and reported high or moderate effect sizes in some studies. However, it seems that this latter meta-analysis included studies in which achievement measures were not always the same in experimental and control conditions. Another methodological issue was raised by Clark (1985): in many quasi-experimental studies of technology integration, instruction in experimental condition is pitted against traditional instruction. This often means that, aside from integration of technology, experimental instruction is based on the latest theories of instructional design while instructors in control condition teach as they have always taught. Thus, it is possible that instruction in experimental conditions would have the same, hopefully beneficial, effect with or without the integration of technology. Lowe (2001) provides evidence that this may be the case in many studies. He found no significant differences between CAI and traditional instruction (without computers) when the instructor was the same in both experimental and control conditions. In addition, instructor-assigned grades are often used as achievement measures in studies of effectiveness of CAI. Such grades may not be reliable measures as Dedic, Rosenfield and Ivanov (2008) demonstrated in their study. In this study, the instructional design for all three conditions was controlled and achievement, measured based on coding done by independent coders, was independent of instructor grading.

The importance of homework as a crucial element of improved instruction has been established in many meta-analytical studies (e.g., Warton, 2001). Currently, in typical college mathematics courses the teacher lectures, and then assigns homework (part of summative assessment) that can only be solved with an understanding of lecture content. In this context, students must self-monitor success and self-correct understanding until new concepts are mastered. Only highly self-efficacious students possessing appropriate self-regulatory strategies thrive in this type of environment (Zimmermann and Pons-Martinez, 1992). The key missing component is effective feedback to/from students from/to teachers during learning (Buttler and Winne, 1995). The Web’s accessibility has given rise to Web-based online assignment systems providing instant feedback to students, perhaps shifting the emphasis from summative towards formative assessment, particularly when multiple tries are permitted (Pollanen, 2007). Most of these systems are proprietary to textbook publishers and reports concerning the impact of their use on students’ achievement are not available. However, the award-winning online assignment system, WeBWorK, available free of charge from the University of Rochester , has been adopted by a large number of institutions in USA and Canada . WeBWorK has features that make it attractive for mathematics educators. First, students cannot simply copy solutions because each student is assigned problems containing randomized parameter values. Second, a large collection of ready-to-use problem sets is available in the WeBWorK database (problem sets have been assembled by a large number of mathematical educators and tested on thousands of students, and new problems are constantly generated, discussed and shared within the WeBWorK user community). Third, the evaluation routines allow for problems where the expected answers are: numbers, functions, symbolic expressions, arrays of yes/no statements, multiple choice questions, etc. Finally, statistical information concerning students’ progress, automatically generated by the system, is available in real time so that instructors can practice “just in time teaching”.

The impact of the use of this system on students has been studied (e.g., Gage, Pizer and Roth, 2002; Weibel and Hirsch, 2002; Hauk and Segalla, 2004; Segalla and Safer, 2006). Some of these studies determined that using WeBWorK to deliver homework problems significantly improved the academic achievement of those students who in the end actually did the homework. Thus, usage of this system might address key issues such as the timing of teacher feedback to students and student feedback to teachers, while providing the possibility for copious amounts of practice for students without increasing the burden of grading. Research into the impact of using Web-based homework systems on student achievement is growing (e.g., Bonham, Beichner & Deardorff, 2001) but the results are as yet inconclusive. It appears that many of these studies failed to control for instructional design differences between control and experimental conditions. In addition, they relied on instructors’ assigned grades, which may not have been unbiased measures of student achievement (Dedic et al., 2008). Since instructors and institutions appear to be eager to implement WeBWorK, the integration of this system into instruction warrants a more carefully designed study. Interestingly, Weibel and Hirsch (2002) also reported student comments that WeBWorK’s instant feedback helped them monitor their own learning progress. Although such comments indicate the positive impact of WeBWorK on student motivation, there was no systematic attempt to measure motivation, or even to collect such comments in that study.

Note that instructors tend to attribute high failure rates in Calculus to students’ low motivation towards both studying and working through assignments. Claims concerning student amotivation fall into the domain of motivational theorists. In social cognitive theory (Bandura, 1997), self-efficacy, personal judgement of one’s capability to accomplish a task, stands out prominently as having the greatest direct mediating effect on human psycho-social functioning. Domain specific self-efficacy beliefs have been shown to correlate positively with achievement in mathematics (Pajares & Miller, 1995) and persistence in academic tasks (Pajares, 2002). Mathematical self-efficacy beliefs of female students are usually lower than those of male peers (Pajares, 2002) and tend to further decrease in Calculus (Rosenfield, Dedic, Dickie, Aulls, Rosenfield, Koestner, Krishtalka, Milkman, & Abrami, 2005). It is possible to anticipate that prompt feedback, as offered by WeBWorK, along with the option to try again, may raise student self-efficacy.

According to self-determination theory (Deci & Ryan, 2000), learning environments promoting student autonomy positively impact on student motivation to strive for higher achievement. When students feel autonomous, competent and related, their self-efficacy rises, and consequently they tend to persevere in their studies. Perceptions of autonomy-supportive learning environments were observed to correlate with perseverance of college science students (Dedic, Rosenfield, Simon, Dickie & Ivanov, 2007). It is possible that just using an online assessment tool with multiple tries and having no other instructional design innovations may stimulate student perceptions of being in control. However, it was postulated that using WeBWorK in the classroom setting might further promote motivation by allowing instructors to provide elaborative feedback and thus raise students’ self-efficacy and achievement. Additionally, using WeBWorK in classroom might generate interactive learning environments that have been shown (e.g., Hake, 1998) to promote deeper conceptual understanding; hence, this design may augment the impact of using an online assessment tool.

Thus, the objective of this quasi-experimental study was to study whether an implementation of WeBWorK, combined with in-class interactive sessions, would promote student achievement and motivation more than the simple addition of WeBWorK homework problems, and again more than the traditional use paper-based homework assignments. In addition, the objective of this study was to avoid pitfalls of similar studies by both controlling the instructional design across all conditions and using instructor-independent measures of achievement, and thus contribute to the understanding of effective use of computers in education.

Methodology

Sample

Participants were 354 social science students (42.1% women; 57.9% men) enrolled in nine Differential Calculus classes, all given in the same semester at a two-year junior college. Over 95% of the students signed a consent form agreeing to participate in this experiment. Most of the students in this study intended to continue their studies at University in the social sciences following graduation from college. Eight instructors, teaching those nine intact classes of Calculus, also agreed to participate. Based on instructors’ preference for the instructional design, three classes were assigned to each of the three experimental conditions. Thus, 118 (38.1% women, 61.9% men) student participants were enrolled in experimental Condition C1; 114 (38.6% women, 61.4% men) students were enrolled in Condition C2; and 122 (49.2% women, 50.8% men) students were enrolled in Condition C3. Students knew nothing of the differences between classes prior to the beginning of the semester. Thus, experimental condition could not have influenced students’ choice of section at registration.

Procedure

Participating instructors agreed to use a similar instructional design. To this end, they agreed to use a common textbook, the same course evaluation schema and the same ten problem assignments. They met regularly during the semester and agreed to maintain the same pace in all sections. Each teacher gave three term tests containing some questions common across all sections and a comprehensive common final examination. Participating instructors also agreed to administer two questionnaires (the first one during the first week of classes and the second one during the last two weeks of classes). The first questionnaire assessed student prior knowledge of mathematics and prior motivation. The second questionnaire assessed students’ perceptions of the learning environment as well as post-instruction motivation.

The differences between the three conditions were as follows. The three instructors in C1 lectured in class and assigned paper versions of problem sets, returned (simple correct/incorrect marking to mimic that of WeBWorK) one week after submission. The two instructors in C2 also lectured in class, but assignments were WeBWorK-based, with an unlimited number of tries. Thus, students in C2 obtained instantaneous feedback (correct/incorrect) from WeBWorK and were encouraged to try again when their solution was incorrect, or to seek help from peers or teachers. Condition C3 differed from C2 solely in that the three instructors engaged students to work on WeBWorK-based assignments for approximately one hour per week (20% of class time) in a computer lab. During these in-class interactive sessions students were encouraged to seek help from the instructor or from their peers, while working either alone or in groups with computers.

Students were not randomly assigned to conditions in this quasi-experimental study. Since, theoretically, differences in various student characteristics (prior achievement, prior knowledge of algebra and functions, prior self-efficacy, prior self-determined motivation, prior extrinsically determined motivation, and prior amotivation) were likely to impact on achievement outcomes or motivational outcomes, it was deemed necessary to first examine such differences. Further, instructors selected which experimental condition suited their teaching style. Since a teaching style is likely to impact on learning environment, and since students’ perceptions of autonomy-supportive learning environment were previously found to impact directly on self-efficacy and indirectly, on achievement (Dedic, Rosenfield, Simon, Dickie, Ivanov & Rosenfield, 2007), it was deemed necessary to also assess student perceptions (Perceptions of Autonomy). When prior differences or differences in students’ perceptions were found, univariate or multivariate analysis of covariance could be used in the analysis of outcomes. Given the expectance of gender differences in both achievement and motivational outcomes in mathematics courses, gender differences were also examined in this study. The GLM algorithm was used with two independent factors: Condition (levels: C1, C2, C3) and Gender (levels: women, men). During the course of this experiment, to gain further insight into the conditions, a one hour structured interview was held with instructors in each of the three conditions.

Measures: Knowledge and Achievement

Student prior achievement (High School Math Performance) was computed as the average grade (scale 0 to 100) in high school mathematics courses. Two instruments, Knowledge of Algebra and Knowledge of Functions (Dedic et al., 2008), were used to measure students’ pre-Calculus mathematical knowledge. These scales assessed the probability of all answers being correct on each of these two instruments.

Students’ achievement in Calculus (fscore) was assessed independently of instructors’ grading practices by coding (two coders; 92% inter-coder reliability) and scoring 13 common problems from the three term tests and 10 problems from the common final examination. In addition, the percentage of correctly solved assignment problems (Assignment) was assessed. Variables fscore and Assignment varied from 0 to 100 (all problems solved correctly). The data used to compute Assignment were reported by an independent coder in condition C1, or in conditions C2 and C3, uploaded from the files available in the WeBWorK system.

Measures: Motivation and Self-efficacy

Student motivation was assessed using an adapted Academic Motivation Scale (AMS) (Vallerand, Pelletier, Blais, Brière, Senécal & Vaillieres, 1992). The AMS was found reliable and valid in the past with Cronbach’s alphas ranging from .70 to .89 (Vallerand et al., 1992) This multidimensional scale was adapted, in consultation with the AMS authors, to assess reasons for taking a Calculus course. The 8-item scale (α-Cronbach = .823), Self-determined Motivation, reflects both intrinsic motivation (e.g.,I study Calculus because I get pleasure from learning new things in Calculus.) and identified regulation (e.g., I study Calculus because I think that knowledge of Calculus will help me in my chosen career.). The 8-item scale (α-Cronbach = .786), Extrinsically Determined Motivation, reflects both external regulation (e.g., I study Calculus because without Calculus it would be harder to get into university programs that lead to high-paying jobs.) and introjected regulation (e.g., I study Calculus to prove to myself that I am capable of passing a Calculus course.). The 4-item Amotivation scale (α-Cronbach = .877) assesses students’ lack of motivation to study Calculus (e.g., Honestly, I really feel that I am wasting my time in a Calculus course.).

Students’ mathematical Self-efficacy was assessed using a 6-item instrument that was adapted from the MSLQ (Pintrich, Smith, Garcia, & McKeachie, 1991) in previous studies (Rosenfield, Dedic, Dickie, Aulls, Rosenfield, Koestner, Krishtalka, Milkman & Abrami, 2005). Items specifically refer to student beliefs about their competence in Calculus (e.g., I am confident that I will be able to correctly solve problems in Calculus.). This instrument was found to have a high internal consistency in this study (α-Cronbach = .83) and was previously shown to have external validity (Rosenfield et al.,, 2005). All instruments employed in this study used 5-point Likert scales.

Measures: Student Perceptions of Learning Environment

A 9-item instrument (e.g., The teacher tried to ensure that students felt confident and competent in the course.), that was originally adapted from the Perceptions of Science Class Questionnaire (Kardash & Wallace, 2001), was used. This instrument was found to have high internal consistency in this study (α-Cronbach = .89) and external validity (Rosenfield et al., 2005).

Results

Initial Analysis

First, the data set was tested for the presence of univariate/multivariate outliers and twenty-two outliers were removed from analysis. Then, differences in prior knowledge were examined using multivariate analysis of variance. This analysis revealed one significant main effect (Condition) on a linear combination of DVs (High School Math Performance, Knowledge of Algebra and Knowledge of Functions) (F(6,279)=4.674, p<.001, Partial η 2 = .048). Tests between subjects showed that only the mean of Knowledge of Functions was significantly lower in C2 (M=.04) in contrast with C3 (M=.16), and in contrast with C1 (M=.19). This indicates that there were no significant differences between the means in three conditions on two variables assessing the prior knowledge (High School Math Performance and Knowledge of Algebra). Furthermore, this indicates that there were no significant differences in the prior Knowledge of Functions between students in condition C1 and C3. Nor were there any significant differences in prior knowledge between genders. Next, differences in prior self-efficacy and motivation were examined using a multivariate analysis of variance. This analysis revealed two significant main effects (Condition, Gender) on a linear combination of DVs (Prior Self-efficacy, Prior Self-determined Motivation, Prior Extrinsically Determined Motivation and Prior Amotivation) (F(8,311)=1.960, p=.049, Partial η 2=.025 and .F(4,311)=6.103, p<.001 Partial η 2=.073 resp.) indicating a small strength of association between variables. Tests between subjects indicated the mean of Prior Amotivation was higher in C2 (M=1.845) in contrast with C3 (M=1.622) and C1 (M=1.512) and the mean of Prior Self-determined Motivation was lower in C2 (M=3.428) in contrast with C1 (M=3.692). In addition, both mean Prior Self-efficacy (M=3.338) and Prior Extrinsically Determined Motivation (M=3.298) of women were lower than the corresponding means for men (M=3.666 and M=3.492). Finally, student perceptions of learning environments were examined using a univariate analysis of variance. This last analysis revealed neither significant main effects (Condition, Gender) nor interaction effects (Condition*Gender).

In summary, these results indicate small differences in both prior knowledge and prior motivation between conditions and between genders. Since all effect sizes were small, this indicates that only a small fraction of variance (less than 10% in each case) could be explained if any of these variables were to be included in further analysis. On the other hand, the cumulative effect of lower prior knowledge of functions, lower prior self-determined motivation and higher prior amotivation of C2 students raise some concern that the achievement of C2 students could be underestimated if those variables were not included as covariates in further analysis. To avoid this possibility, these variables were included in the subsequent analysis, but perceptions of learning environment were not.

Impact of Condition on Student Achievement

A univariate analysis of covariance was used separately to assess the impact of condition and gender on two student achievement variables (fscore and Assignment). In both cases, the covariates included prior achievement variables (High School Math Performance, Knowledge of Algebra and Knowledge of Functions) and prior motivational variables (Self-efficacy, Self-determined Motivation, Extrinsically Determined Motivation and Amotivation). The first ANCOVA that examined the effect of Condition and Gender on fscore revealed one significant main effect (Condition: F(2,256)=12.127, p<.001, Partial η 2 = .087). The effect size indicates a modest association between Condition and fscore. Tests between subjects showed that C3 students outperformed both C1 students (M(C3)-M(C1)=58.931-49.180=9.751) and C2 students (M(C3)-M(C2)=58.931-46.196=12.735). Figure 1 illustrates these differences.

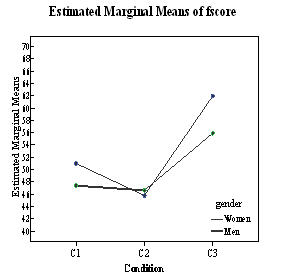
Figure 1.

Although there was no significant gender effect or interaction Condition*Gender effect, marginal means indicated that there were gender differences in conditions C1 and C3. Consequently, these differences were scrutinized by examining the population of students in conditions C1 and C3 separately. It was found that gender differences were not significant in condition C1. However, analysis of variance revealed that women (M=63.4) significantly (F(1,114)=9.962, p=.002) outperformed men (M=50.3) in condition C3. When prior differences were taken into account, analysis of covariance showed that women (M=64.3) outperformed (F(1,88)=3.467, p=.066) men (M=56.3) in condition C3, but the differences were not significant. Note that the marginal means above are not the same as those in the Figure 1. This is because this analysis of covariance was done on the population of students in condition C3 alone as opposed to the entire population of students, i.e., conditions C1, C2 and C3.

Analysis of covariance of student performance with Assignment as dependent variable revealed similar results. Condition significantly affected student performance on assignments (F(2,270)=27.647, p<.001, Partial η 2=.176), showing a moderate association between Condition and student grades on assignments. Students in condition C3 again outperformed students in both condition C1 (M(C3)-M(C1) = 80.555-63.467 = 17.088) and students in condition C2 (M(C3)-M(C2) = 80.555-61.368 = 19.187).

Impact of Condition on Student Motivation

A multivariate analysis of covariance with all prior motivation variables as covariates revealed no significant main effects or interaction effect on combined DVs (Post Self-efficacy, Post Self-determined Motivation, Post Extrinsically Determined Motivation and Post Amotivation). However, there was a significant effect of Condition (F(2,225)=3.349, p=.034, Partial η 2=.031) and a significant effect of interaction Condition*Gender on Post Self-efficacy (F(2,225)=3.052, p=.049, Partial η 2=.028). The effect size indicates that both of these effects are very small. Tests of self-efficacy between subjects showed that C2 students had significantly lower post self-efficacy beliefs than C3 students (M(C2)-M(C3)=3.365-3.083=-.282). Figure 2 shows that men’s post self-efficacy was the same across all three conditions. Thus, the fact that, on average, C3 students believed in their competence significantly more than C2 students did is caused by the heightened self-efficacy of C3 women. Women’s post-instruction self-efficacy was significantly higher than that of C3 men.

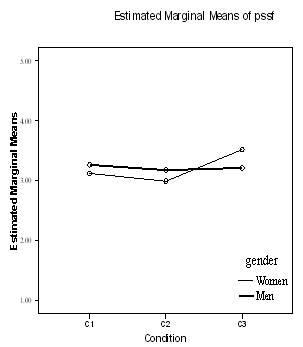
Figure 2.

The table below shows how student beliefs about their competence in mathematics have changed over the course of the semester. It is noteworthy that Self-efficacy declined significantly for men in all conditions and for women in conditions C1 and C2, but not for women in C3.

Post-experiment Interviews

Instructors indicated their satisfaction with the collaboration that took place during the course of this experiment and felt that there was a great similarity in Calculus instruction in all sections. They also stated that they intend to use the C3 instructional strategy in future. C1 instructors expressed concerns that their students copied solutions. C3 instructors reported a deluge of student e-mails asking about assignment questions while C1 and C2 instructors reported that students rarely sought help outside of class.

Discussion

In discussing the results of this study, it is important to reiterate that achievement was uniformly measured in all three conditions in this study. Furthermore, by using analysis of covariance, prior differences in student achievement and motivations were statistically accounted for. Thus, it is reasonable to attribute post-result differences in achievement to the differences amongst the three conditions. Given that instructors perceived that they taught using a common instructional design, it is also evident that the mode of assignment delivery (paper vs. WeBWorK), and feedback promptness (one week versus instantaneous) distinguished C1 and C2 and that weekly one-hour interactive sessions distinguished C3 and C2.

The lack of significant differences in student achievement (fscore) between C1 and C2 indicates that using computers to deliver assignments and to provide prompt feedback has no impact on students’ learning of Calculus. This in itself is a positive result since using computers in this manner allows instructors to assign (more) problems without being overburdened. This result confirms the findings of the meta-analysis of studies by Bernard et al. (2007) and Christmann and Badgett (2000), both of which found a number of studies reporting no significant differences between CAI and traditional instruction. Both of these meta-analyses report a small average positive effect size, but in this study, probably because instructional design was tightly controlled across conditions, no such positive effect is seen.

There were also no significant differences in student achievement on assignments between conditions C1 and C2. This finding is corroborated by instructors who did not observe that their students in either condition were exerting unusual effort. Although means were close to 60% in both conditions, indicating that many students were having difficulty with the assignments, these students rarely sought the help of instructors outside the classroom. In terms of student self-efficacy, in both conditions, student self-efficacy significantly decreased. No other changes in motivation were observed in either condition. Weibel and Hirsch (2002) reported anecdotal student comments to the effect that instant feedback helps them to monitor their progress. Thus, it was hypothesized a priori that the instant feedback of WeBWorK would positively impact on student motivation. However, the results show that the only such impact was in condition C3, indicating that the hypothesized mechanism of instant feedback leading to higher motivation was not observed.

As shown above, condition C3 had a significant positive impact on student achievement. Students in this condition outperformed students in the other two conditions by a large margin. Although the effect size was moderate (8.7% of variance explained), we conclude that students in this condition learned more. Thus, spending 20% of class time providing additional instructional support to students working on problem sets is worthwhile. These results support Lowe’s (2001) conclusion that CAI is not a panacea, but rather a tool that can be used to enhance an effective instructional strategy.

As observed above, students in condition C3 outperformed other students on assignments by a large margin, hence most students in C3 were not experiencing difficulty with the assignments. Despite this, C3 instructors reported that many of their students frequently sought assistance outside the classroom. C2 instructors did not observe a similar phenomenon. Since computers were used to deliver a prompt feedback in both conditions we speculate that additional instructional support for the use of computers given in condition C3 stimulated student effort. This finding supports the idea proposed by Lowe and Holton (2005) that a successful implementation of CAI requires appropriate instructional support. Although all students performed better in condition C3, as noted above, women in particular thrived in this learning environment. While the self-efficacy of men decreased in C3 in a fashion similar to the other conditions, the post self-efficacy of women in C3 remained stable. Consequently, the post self-efficacy of women was significantly higher than that of men. Lower self-efficacy of women in mathematics, as reported by most studies, is often cited as the reason for lower enrolments of women in mathematics courses. If this is really the case, then it is anticipated that CAI implementations similar to condition C3 might lead more women to take more courses in mathematics.

The fact that, in post instruction interviews, all instructors in this experiment indicated that they now employ the C3 instructional design is an extraordinary result on its own, because recommendations coming from educational research often have little impact on actual teaching (Handelsman et al., 2004). Although this design requires schools to have a sufficient number of computer labs with either LAN or Internet connections, this may not be an impediment to implementation because many colleges and universities already have such classrooms.

Limitations

This study is not a full 2x2 design, thus it is not possible to disentangle the differential impact of WeBWorK and interactive sessions. Furthermore, the collected data do not provide an explanation concerning how the instructional design in condition C3 promoted student learning. The assessment of student perceptions of learning environments was based on the self-determination theory of Deci and Ryan (2000). This measure did not show any significant differences between conditions. This may mean that autonomy support is not the mechanism which led students in condition C3 to exert more effort. The authors speculate that such a mechanism may involve: reduced intimidation, allowing students to ask questions; additional explanations from their instructor focussed on their individual needs; heavier emphasis on doing assignments, by virtue of spending class time on them, thereby validating the worth of assignments in the eyes of students; easy initiation to working with peers. Further research is needed to clarify the exact mechanism(s) involved.

Conclusion

This study indicates that the downward trend in student achievement in Calculus is reversible by promoting instructional designs similar to C3. Since virtually all mathematics instructors believe that “practice makes perfect” and since a large number of schools already employ WeBWorK, implementing a C3 design across many colleges or universities should not encounter much resistance from faculty or administrations. In addition, the results show that student efforts in this condition were significantly higher than the efforts of their peers in the two other experimental conditions. While delivering and grading assignments via a computer is an efficient alternative to employing human markers, this research indicates that providing feedback via WeBWorK alone is not enough to improve student achievement or to promote larger effort on their part. Alas, the collected data does not provide evidence for any particular mechanism by which the performance of C3 students improved.

The three conditions were examined to determine if they had a differential impact on student motivation and self-efficacy. It was determined that it did not when prior motivation was controlled for. However, it was found that the self-efficacy of women in classes that included interactive sessions was higher than the self-efficacy of men. It is possible that this effect is due to the fact that women in C3 significantly outperformed men. That is, it could be that the self-efficacy of women rose because they experienced or witnessed success. It is also possible that additional feedback they obtained from their peers and the instructors during the interactive sessions contributed to their increased beliefs about their competence and offset their traditional discomfort when computers are integrated in classes ( Butler , 2000).

The rigorous methodology used in this study, including uniformity in pedagogy, uniform assessment of student achievement and control for prior differences among experimental conditions allows us to be confident of the validity of results in this study. In this manner, this study is a contribution to the growing knowledge concerning CAI. In addition, one should note that the content of the course was very traditional. Despite the advice of researchers in mathematics education that the content of the Calculus course needs to be reduced, the content remained intact in the context of this study.

Although, the C3 instructional strategy was tested amongst college social science students, there is nothing specific about this population or strategy that would indicate that this strategy would fail to impact similarly on university or college science students. A modest investment in technology, combined with in-class interactive sessions, could reverse the current trends of decreasing enrolment and high failure rates in introductory mathematics classes. This is the most important result of this research.

Acknowledgement

The research reported on in this paper was carried out under a grant from PAREA and the Ministry of Education, Leisure and Sports, Quebec . We wish to thank the participating instructors for their kind cooperation in helping us carry out this study. A final word of thanks is due to Dr. I. Alalouf, Université du Québec à Montréal, for his patient guidance in all matters statistical.

References

Ball, D. L. & Forzani, F. M. (2007). What Makes Education Research “Educational”? Educational Researcher, 36(9), 529-540.

Bandura, A. (1997). The Self-efficacy: The Exercise of Control. New York Press: Freeman.

Bernard, R. M., Abrami, P. C. & Wade, C. A. (2007). A Summary of “Review of E-learning in Canada : A Rough Sketch of the Evidence, Gaps and Promising Directions”. Horizons, 9(2), 32-36.

Bonham, S., Beichner, R. & Deardorff, D. (2001). Online homework: Does it make a difference? The Physics Teacher, 39, 293-296.

Buttler, D. L. & Winne, P. H. (1995). Feedback and Self-regulated Learning: A Theoretical Synthesis. Review of Educational Research, 65, 3, 245-281.

Butler , D. (2000). Gender, Girls, and Computer Technology: What's the Status Now? The Clearing House , March/April 2000, 225-229.

Christmann, E. & Badgett, J. (2000). The Comparative Effectiveness of CAI on Collegiate Academic Performance. Journal of Computing in Higher Education, 11(2), 91-103.

Clark, R. (1985). Evidence for confounding in computer-based instruction studies: Analyzing the meta-analyses. Educational Technology Research and Development, 33(4), 249-262

Deci, E. L. & Ryan, R. M., (2000). Intrinsic and extrinsic motivations: Classic definitions and new directions. Contemporary Educational Psychology, 25, 54-67.

Dedic, H., Rosenfield, S., Simon, R., Dickie, L., Ivanov, I. & Rosenfield, E. (2007). A Motivational Model of Post-Secondary Science Student: Achievement and Persistence. Paper presented at the April 2007 annual meeting of the American Educational Research Association, Chicago.

Dedic, H., Rosenfield, S. & Ivanov, I. , (2008). Online Assessments and Interactive Classroom Sessions: A Potent Prescription for Ailing Success Rates in Social Science Calculus, PAREA report, Quebec , ISBN 978-2-921024-84-5

Gage, E. M., Pizer, A. K., & Roth, V. (2002). WeBWorK: Generating, Delivering, and Checking Math Homework via the Internet. Proceedings of 2 nd International Conference on the Teaching of Mathematics, Hersonissos , Greece .

Gordon, S. P. (2005). Preparing Students for Calculus in the Twenty First Century. MAA Notes: A Fresh Start for Collegiate Mathematics: Rethinking the Courses Below Calculus. N. B. Hastings, S. P. Gordon, F. S. Gordon & J. Narayan (Eds.) (in press)

Hake, R. (1998). Interactive-engagement vs. traditional methods: A six-thousand-student survey of mechanics test data for introductory physics courses. American Journal of Physics, 66, 64-74.

Handelsman, J., Ebert-May, D., Beichner, R., Bruns, P., Chang, A., DeHaan, R., Gentile, J.,Lauffer, S., Stewart, J.,Tilghman, S. M. & Wood, W. B. (2004). Scientific Teaching. Science 304 (23) 521-522.

Hauk, S. & Segalla, A. (2005). Student Perceptions of the Web-based Homework Program WeBWorK in Moderate Enrolment College Algebra Classes. Journal of Computers in Mathematcs and Science Teaching, 24(3), 229-253.

Hodgson, B. R. (1987). Evolution in the teaching of Calculus. In L. A. Steen (Ed.), Calculus for a new century (pp. 49-50). Washington , DC : The Mathematical Association of America .

Kardash, C. A. & Wallace, M. L. (2001). The perceptions of science classes survey: What undergraduate science reform efforts really need to address. Journal of Educational Psychology, 93(1), 199-210.

Kirschner, P. A., Sweller, J. & Clark, R. E. (2006). Why Minimal Guidance During Instruction Does Not Work: An Analysis of the Failure of Constructivist, Discovery, Problem-Based, Experiential, and Inquiry-Based Teaching. Educational Psychologist, 4(2), 75-86.

Klein, D. & Rosen, J. (1996). Calculus Reform - For the $Millions. Notices of the AMS, 44, 6, 1324-1325.

Kulik, J. (2003). Effects of Using Instructional Technology in Colleges and Universities: What Controlled Studies Evaluation Studies Say? http://www.sri.com/policy/csted/reports/sandt/it/Kulik_ITinK-12_Main_Report.pdf Accessed Aug. 10, 2008

Lowe, J. (2001). Computer-based education: Is it a panacea? Journal of Research on Technology in Education, 34(2), 163-171.

Lowe and Holton (2005). A Theory of Effective Computer-Based Instruction for Adults. Human Resource Development Review, Vol. 4, No. 2, 159-188.

Meyer, R. E. (2004). Should There Be a Three-Strikes Rule Against Pure Discovery Learning? American Psychologist, 59(1), 14-19.

National Centre for Education Statistics (2006). U. S. Student and Adult Performance on International Educational Achievement. http://nces.ed.gov//pubs2006/2006073.pdf Accessed Aug. 10, 2008

Pajares, F. & Miller, M. D. (1995). Mathematics self-efficacy and mathematics performance: The need for specificity of assessment. Journal of Counseling Psychology, 42(2), 1-9.

Pajares, F. (2002). Gender and perceived self-efficacy in self-regulated learning. http://www.findarticles.com/cf_dls/m0NQM/2_41/90190499/print.jhtml (Accessed August 20, 2008 )

Pintrich, P. R., Smith, D. A. F., Garcia, T. & McKeachie, W. J. (1991). A Manual for the Useof the Motivated Strategies for Learning Questionnaire (MSLQ). National Centre for Research to Improve Postsecondary Teaching and Learning, Ann Arbor , MI .

Pollanen, M. (2007). Improving Learner Motivation with Online Assignments. MERLOT Journal of Online Learning and Teaching, 3(2), 203-213.

Rosenfield, S., Dedic, H., Dickie, L., Aulls, M., Rosenfield, E., Koestner, R., Krishtalka, A., Milkman, K. & Abrami, P. (2005). Étude des facteurs aptes  influencer la réussite et la persévérance dans les programmes des sciences aux cégeps anglophones. Final report submitted to FQRSC. ISBN 2-921024-69-1.

Segalla, A. & Safer, A. (2006). Web-based mathematics Homework: A Case Study Using WeBWorK in College Algebra Classes. http://www.exchangesjournal.org/print/print_1193.html (Accessed August 20, 2008 )

Statistics Canada and Organisation for Economic Cooperation and Development (OECD) (2005). Learning a Living.http://www.statcan.ca/english/freepub/89-603-XIE/2005001/pdf/89-603-XWE-part1.pdf (Accessed August 10, 2008 ).

Vallerand, R. J., Pelletier, L. G., Blais, M. R., Bri  re, N. M., Senécal, C. S., & Vaillieres, E. F. (1992). Academic Motivation Scale (Ams-C 28) College (Cegep) Version. Educational and Psychological Measurement, 52-53, 5-9.

Warton, P. M. (2001). The forgotten voices in homework: Views of students. Educational Psychologist, 36(3), 155-165.

Weibel, C. & Hirsch, L. (2002). Effectiveness of WeBWorK, a web-based homework system. http://math.rutgers.edu/~weibel/studies.html (Accessed August 20, 2008 .)

Zimmerman, B. J., & Martinez-Pons, M. (1992). Perceptions of efficacy and strategy use in the self-regulation of learning. In D. H. Schunk & J. L. Meece Ieds.). Student perceptions in the classroom. (pp. 185-207). Hillsdale , NJ : Erlbaum.