Introduction
A common suggestion for getting students involved
in their own learning is to have the students work
together in small groups on assignments. There is
considerable research evidence that the use of
small groups is beneficial to students in
undergraduate science, technology, engineering,
and mathematics (STEM) courses. Springer, Stanne,
and Donovan (1999) conducted a meta-analysis of
studies pitting the use of small-groups against
individualized approaches, and they reported that
the students working in small-groups tended to
have higher levels of achievement and persistence,
as well as more positive attitudes toward the
courses. Davidson, Reynolds, and Rogers (2001)
argue for the use of collaborative groups in
undergraduate mathematics courses, noting several
benefits. A general benefit of collaboration is
the development of interpersonal skills required
to work successfully within a group. More
specifically, Davidson, Reynolds, and Rogers argue
that students can learn from the different
perspectives provided by their group members, and
the process of explaining ideas and concepts to
others often improves one’s own understanding.
Furthermore, the requirement that students work in
groups for mathematical problem solving might
promote the view of mathematics as a human
activity and challenge beliefs that all
mathematical problems have single correct
solutions that can be obtained by routine
procedures.
Potential Difficulties with Asynchronous
Collaborative Problem Solving
While there are many challenges to successful
face-to-face collaborative problem solving, a
separation of time and space creates a new set of
difficulties for using group activities in an
online environment. There are tools that allow
students to communicate by audio, video, text, or
multimedia in real time, but one argued advantage
of online education is a greater amount of freedom
for students to work on their own schedules.
Therefore, it is important to investigate ways to
facilitate problem solving in an asynchronous
setting. For the purpose of this paper, the term
asynchronous refers to any form of communication
that does not occur in real time.
There is an extensive research base documenting
obstacles to meaningful participation in
asynchronous assignments. Harasim (1986) cites a
loss of visual cues, the difficulty and time
needed to reach a group consensus online, health
problems such as eyestrain and backstrain, and a
variety of problems related to technology as
disadvantages of online instruction. Bullen (1998)
investigated student perceptions of factors
influencing participation in an online computer
science ethics course and developed a conceptual
framework with four categories: attributes of the
medium, design of the learning activities, student
dispositional factors, and student situational
factors. Bullen identified many potential
obstacles to online participation in each of these
categories. The purpose of this paper is to
discuss a particular difficulty that arises in
online problem solving when there is a perceived
“correct” answer and to address a potential
approach to combating this difficulty.
A common tool for facilitating asynchronous
communication over the Internet has been a
discussion board. With traditional discussion
boards, once a message is created, it is stored by
an online server and retrievable by anyone with
access to the discussion board. While it is easy
to imagine such a communication tool facilitating
a lively discussion or debate in a humanities or
social science course, it seems more problematic
to use a discussion board for collaborative
problem solving in a STEM course. Although many
educators recommend the use of open-ended problems
with no clearly correct solution or multiple
correct solutions, many problems used in STEM
classes are closed ended with single correct
answers. Such problems may be ill suited for use
with traditional discussion boards. Instead of
proposing ideas, asking questions, or starting
general discussions, students in the author’s
College Algebra classes have tended to post
proposed solutions. Once a solution that is
perceived to be correct has been posted,
discussion tends to stop or becomes limited to
statements of agreement. This type of behavior
leads to two problems commonly found with any form
of group work. Either a small number of students
dominate the discussions without providing
opportunities for others, or certain group members
willingly allow other students to do all of the
work without contributing. One potential solution
to this problem is a two-phase approach such as
that used by Thomas Banchoff (2005) with his
“communication tensor.”
Banchoff’s Communication Tensor
Thomas Banchoff (2005) uses a course management
system that he developed, especially for
mathematics courses, with his students at
Brown
University.
The main tool for facilitating student work in
Banchoff’s software is called the communication
tensor or the tensor for short. Banchoff calls it
a tensor because student work is stored and
displayed in a multidimensional array. When a user
accesses the main webpage for the tensor, he or
she sees a two-dimensional array with a row for
each assignment and a column for each student. By
clicking on an assignment name, the user is taken
to a webpage with another array broken down by
individual problems. Figure 1 shows the
instructor’s view of the tensor in a class with 5
assignments and 13 students. The color codes
indicate whether the instructor or a student made
the last post in an assignment space.

Figure 1.
An instructor’s view of the assignment array in
Banchoff’s communication tensor for
a class with 13 students and five assignments.
Blank spaces indicate that no posts have been
made.
While the row by column format of organizing the
students’ work is a novel approach, the real
innovation of Banchoff’s communication tensor is
the way that assignments are divided into
individual and whole class phases. When an
assignment is written using Banchoff’s software,
the instructor is given the option to set a timed
lock that controls when access will be granted to
the whole class. If an assignment is locked, each
student’s work is only accessible to that student
and the instructor. Once an assignment is
unlocked, any user can access any student’s work
by clicking on a colored square in the tensor.
There is a feature that allows the students to
create private posts that can only be viewed by
the student who makes the post and the instructor
at all times, but the students are encouraged to
make public posts and share as much as possible.
Figure 2 shows a sample screenshot from the
perspective of a student with user name ds.
Because the assignment labeled “Optimization” is
locked for the initial phase, the student cannot
see hyperlinks to his classmates’ work. Each of
the other assignments is unlocked, and the student
can see a hyperlink for each student who has
attempted the problems.

Figure 2.
The view of the assignment array in Banchoff’s
communication tensor for a class with
five assignments and 13 students from the
perspective of a student with the username ds.
The assignment labeled Optimization is locked and
the other assignments are unlocked.
The Shared-Work Approach
The method of facilitating online problem solving
used by Banchoff with his communication tensor can
be called a “shared-work approach” because each
student is responsible for completing his or her
own assignment in an individual space, and the
students’ work is shared through the tensor. The
students are not assigned to specific groups and
are not explicitly required to collaborate, but
they have access to the shared work to use as they
desire. With the individual initial phase, the
shared-work approach prevents some of the common
problems associated with group work such as one or
more students dominating discussions or students
relying on group members to do all of the work.
Figure 3 provides an example of an assignment on
quadratic modeling from one of the author’s
College Algebra classes and the messages posted by
a student with pseudonym S27 and the author in the
student’s assignment space. The first two messages
were posted during the initial phase when S27 only
had access to her own space. In her first attempt
at the problem, S27 started with the area formula
for a triangle instead of a rectangle, and her
algebra was incorrect. Trying to give just enough
help to keep her working toward a correct
solution, the author made a comment on the area
formulas. S27 did not make another post on this
assignment until the second phase, when the tensor
was open. She then correctly solved the initial
problem, posed her own problem, and solved a
classmate’s problem that she had found in the
tensor. It is worth noting that student S28 had
made up a correct problem, but he had no correct
work toward a solution to his problem or the
original problem.

Figure 3.
The content of student S27’s assignment space for
an assignment on quadratic
modeling used with a communication tensor and a
shared-work approach.
A Small-Groups Version of the Shared-Work Approach
Banchoff’s tensor has the advantage of requiring
individual contributions while providing
opportunities for collaboration. However, based on
the author’s experiences as a student and a
teacher using the tensor, the student-to-student
interactions can be limited when compared to
traditional group work. With the use of individual
assignments, a student’s goal becomes to solve the
assigned problems in his or her own assignment
space. With time constraints and many other
commitments, students tend to look at the other
students work only when they perceive that it is
necessary. When the students in a section of
College Algebra taught by the author using an
individualized shared-work approach were asked how
they had found the tensor helpful (Cooper, 2008),
the most popular responses were that they would
look for help whenever they were stuck or that
they would look at other students’ work to check
their own. When asked why they did not look at the
work of others more often, several students said
that they felt no need to do so when they were
confident in their own work.
In order to promote more student-to-student
interactions while maintaining the advantages of
an individual initial phase, the author has
implemented a small-groups version of the
shared-work approach, using a version of the
tensor with an extra lock for facilitating group
work. In the author’s software, when an assignment
is locked at a group level, each member of a group
can access the work of his or her group members.
This allows an initial phase where students work
alone and a second phase in which they continue to
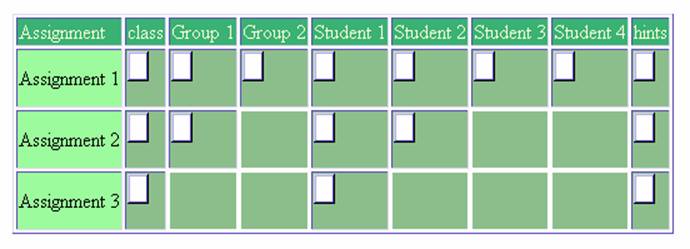
work within small groups. Figure 4 displays a
sample screenshot from the author’s software from
a demonstration class with 4 students and 2
groups. This screenshot is from the perspective of
Student 1, who belongs to Group 1 with Student 2.
Students 3 and 4 make up Group 2. Assignment 3 is
locked at an initial phase, and Student 1 can only
access his own space and areas for hints and
comments for the whole class. Assignment 2 has
progressed to a secondary group phase in which
Student 1 can access his own space as well as
Student 2’s space and their group space.
Assignment 1 is unlocked at the class level, an
option that instructors can use to make all work
on an assignment available to the entire class.
|
Figure 4.
Student 1’s view of the tensor in a small-groups
section using the author’s communication
tensor. Assignment 1 is unlocked at the class
level; Assignment 2 is locked at the class level
but
unlocked for groups; and Assignment 3 is locked
for an individual phase.
The tensor structure is one way to accomplish a
small-groups version of the shared-work approach,
but instructors can use any software that allows
individual submissions (such as e-mail) and
small-group discussions. Figure 5 contains an
outline of the two versions of the shared-work
approach discussed in this article.
Student Assignments
While the term problem is often used in
mathematics to describe any exercise, O’Daffer,
Charles, Cooney, Dossey, and Schielack (2005)
describe a problem as a situation that involves a
question that is challenging to the students and
that cannot be answered immediately by some
routine procedure known to the students. The
author has attempted to use problems in online
assignments that satisfy these criteria. In
addition to presenting non-routine challenges,
problems with multiple correct solutions or
solution strategies are even better. For example,
a routine exercise would be to find an equation
for a line passing through two given points. A
more challenging open-ended assignment is to find
equations of three lines that intersect to form a
triangle with a given area. In a shared-work
approach, students are given time to grapple with
such a question on their own, and then they are
given access to the work of the whole class or a
small group. At the end of the individual phase,
it is likely that several different correct
specific solutions have been found and that
several students have been unable to find a
solution. During the shared-work phase, the
students are exposed to different solutions. The
students who were unable to solve a problem can
observe the strategies used by their classmates
and create their own solutions. Ideally, the
students will discuss general solution strategies
and properties of the assignment. With this type
of assignment, the students get to experience a
problem-solving situation and practice basic
skills. By the time that a student has developed
equations for a triangle with a given area, he or
she has practiced finding an equation of a line
through given points, likely including horizontal
and vertical lines. By using a non-routine
situation the students are given an opportunity to
learn that struggling with an assignment is
acceptable and that mathematics is not simply
about memorizing rules and procedures.
The Shared-Work Approach
Initial Phase
During an initial phase, the students are assigned a set of problems and given access to an online space to construct their individual answers and interact with the instructor. During this phase, the students cannot access any of their classmates’ work on the assignment.
Second Phase- Individual Approach
During a second phase, the students are responsible for finalizing their responses to the problems. Each individual student is responsible for the answers constructed in his or her own assignment space while having access to each classmate’s work.
|
Fi
gure 5. Outline of the individual and
small-group versions of the shared-work approach
to online problem solving.
To date, the author has used the small-groups
approach and the individualized shared-work
approach with the same types of assignments. In an
ideal situation, students working under the
individualized approach would use the whole-class
phase to seek out the work of classmates to
compare and contrast solutions and to discuss the
problems in detail. It has been the author’s
experience that having access to the work of every
student in a class can be overwhelming. Many
students do not have the time or patience to look
at the work of every other student. By using a
small-groups variation of the shared-work
approach, the students still have individual
responsibility, and they are able to focus on the
work of a small number of classmates. It is also
likely that identifying oneself with a group of
three or four classmates will create a stronger
sense of responsibility to the group. Through
experimentation with the two approaches to online
facilitation, the author has found higher levels
of participation and more direct
student-to-student interaction when the students
are placed in small-groups (Cooper, 2008).
Discussion
This paper offers two possible alternatives to
traditional collaboration for use with online
problem solving. The two approaches incorporate a
two-phase method of facilitation to promote
individual accountability and collaboration. The
individualized approach may be appealing to many
instructors. Using the individualized shared-work
approach, the students have the potential to learn
from the work of their classmates, or they may
choose to work independently, interacting with
only the instructor. With the increasing
importance of technology, one could argue that the
students need to be able to decide when and where
to seek information as needed. Deciding what to
look at and how to use what they find in the
tensor may help students develop these types of
skills.
The small-groups version of a shared-work approach
maintains individual accountability, but provides
the students with structured groups. Instead of
sorting through the contents of dozens of
individual student assignment spaces, the students
can focus on working with their small group. The
small-groups approach should also be easier to
adapt to course management systems, such as WebCT,
that do not include a communication tensor. An
instructor could simply set up group discussion
areas and require each student to provide initial
responses by email prior to working in groups.
There are many problems recognized in distance
education that neither of these approaches
eliminates. Mathematical problem solving typically
involves the use of symbols and drawings or
graphs. Entering items other than standard text
into communication software can be difficult and
time consuming. Some students might have
difficulty accessing the required technology, and
some students could require extra help learning
how to use the technology. In addition, it has
been reported that many students view mathematics
as a subject that one does alone with pencil and
paper and that mathematics is about using
memorized procedures to find numerical solutions (Schoenfeld,
1989; Schommer, Crouse, & Rhodes, 1992). It is
difficult to get students to interact and discuss
mathematics if they believe that the only purpose
is to find the single correct answer, but teachers
must work to find ways to push students toward the
development of meaningful understanding. The
approaches to online problem solving described in
this paper are ways that the author has used to
present challenging problems in undergraduate
mathematics classes. Teachers and researchers are
encouraged to explore these approaches and to
continue searching for better tools and methods of
promoting online problem solving.
Acknowledgements
The author would like to thank Thomas Banchoff for
introducing him to the communication tensor and
inspiring the use of appropriate technology in the
classroom.




