Introduction

Students preparing to take college-level mathematics courses are exhibiting a critical shortage of higher-level skills. This nationwide problem is partly attributable to an over-reliance on memorization. Despite the best efforts of many mathematics teachers, the problem is still confounded by using Multiple-Choice (MC) questions in all high-stakes mathematics assessment tests (e.g., for high school graduation or college admission), MC questions have pre-determined correct or incorrect answers, hence mainly focus on retention (Becker & Shimada, 2005), In contrast, problems that allow students to provide their own constructed responses are more challenging, allow multiple variations of the correct answer(s), and lead students to see the beauty and creativity inherent in mathematics (Becker & Shimada, 2005; Jarrett, 2000; Moon & Schulman).

This article presents an innovative mathematical expression parser (U.S. patent pending; Livne, Livne, & Wight, 2007a) that automatically scores students’ constructed responses to mathematical questions at the core of a free college readiness website (http://ruready.net). Each response is compared to an instructor-provided reference expression; each response element is identified as correct vs. missing, unrecognized, wrong, or redundant, and the response is assigned a partial-credit score on a 0-100 scale in real-time. The score reflects both the overall response correctness and the fraction of correct elements identified in the response.

The parser scoring agreed with human teacher scoring to a very high degree of accuracy and was found to be as consistent as human scoring. The parser performed well even when the constructed response assessment was not clear-cut (either totally wrong or totally correct), but lay in a “gray area” that required human expertise to award meaningful partial-credit.

The parser was further used to score additional real-world students’ responses to pre-Calculus questions. The results indicated that students’ errors were factored into two groups: structural vs. computational, reflecting the parser’s ability to distinguish between different error patterns beyond human scoring. 

Literature Survey

Constructed responses to mathematical questions have been recommended as an effective way to enhance students’ ability to organize and communicate knowledge in their own way, as opposed to Multiple-Choice (MC) questions (Becker & Shimada, 2005, Jarrette, 2000; Kristin et al., 2005; National Science Teachers Association, 2005; Pehkonen, 1997). Through constructed responses, students’ incorrect responses are normally awarded partial-credit, whereas MC responses are scored only as correct or incorrect; MC questions invite students to resort to guessing or to solving problems backward, thereby introducing large measurement errors. This limitation not only discourages students from gaining a deep conceptual understanding in mathematics (McIntosh, & Jarrett, 2000; National Research Council, 1999; Paul, 1993), but further leads to discrepancies between human teacher grading and machine grading of the same student response. Human partial-credit scoring of constructed responses reflects the number of learning points that the student has achieved for an answer that is not fully correct; it especially forgives small algebraic or arithmetical errors (Beevers & Paterson, 2002). In contrast, machines face difficulties in extracting such implicit information from the student’s response, and score the final answer only as correct or incorrect, disregarding the range of “intermediate responses” (Ashton, Beevers, Korabinski, & Youngson, 2006; Bennett, Steffen, Singley, Morley, & Jacquemin, 1997). Moreover, many of the current automated scoring systems exhibit significant scoring errors, as indicated by 35% of testing offices in 23 states (CNN, 2007).  

Several programs offer solutions to automatic scoring of constructed mathematical responses. In Praxis I: Online Academic Skills Assessments (Educational Testing Service, 1997), constructed responses to mathematical questions were matched with either one or a small number of pre-specified answers. The response was dichotomously scored by literally matching it against each correct answer, much like multiple choices. Bennett et al. (1997) developed questions that have a single correct answer that may, however, take a large number of forms. Responses were still only scored as correct or incorrect. McGuire, Youngson, Korabinski, and McMillan (2002) offered another type of partial-credit scoring for automated assessment tests that was based on the number of solution steps taken by the learner. For each of four pre-defined steps, the student provided a single solution and either received full credit if the step was solved correctly, or no credit if the step’s solution was incorrect. The total score was the sum of correct step scores. None of the scoring techniques cited above has been validated to be robust, and none agreed with human scoring across a wide range of responses; further, these techniques generated only a final score and could not identify and/or classify specific error types. 

To address these challenges, the University of Utah created RUReady, a free online self-regulated learning and assessment website (http://ruready.net) intended to improve student college-readiness. The core of the software is a mathematical expression parser – a novel analyzing tool that generates comprehensive error analysis and real-time automated partial-credit scoring for each student response. To determine whether the RUReady parser is a valid tool for automated partial-credit scoring in mathematics, two research questions were posed: (1) Can a computer closely match human graders? and (2) Can a machine surpass human graders by distinguishing between different types of errors? Accordingly, this article is divided into three sections. First, the RUReady parser analysis and its scoring algorithms are described (Method). Secondly, the validation of the parser scoring compared against human teacher scoring is reported (Study 1). Thirdly, the ability of the parser scoring model to distinguish between different students’ error-patterns is evaluated (Study 2). Finally, the results are summarized and discussed, leading to conclusions, limitations, and implications for the mathematics teaching community and for the role of artificial intelligence and natural languages in education.

Method

RUReady Parser Analysis Algorithm
The RUReady learning program is based on the theory of learning from error performance (Ohlsson, 1996) and on evidence that error patterns lead to conceptual misunderstandings and lack of proper problem-solving strategies (Babbitt, 1990; Sleight, 2003) as well. (A parser is an object that recognizes the elements of a language and translates each element into a meaningful result).

The parser requires two inputs:

1. Reference: a keyboard-typed string representing the correct answer to the mathematics question. It is provided by instructors and stored in a database.
2. Response: a keyboard-typed string representing a number, mathematical expression or equation. It is provided by a student in real-time.

The parser’s output includes a detailed analysis of the student’s response, consisting of three successive phases:

1. Matching: directing comparison of the elements in the reference and response strings, and reporting whether the response is a legal expression that adheres to standard arithmetic and logical syntax rules.
2. Numerical Evaluation: deciding and reporting whether the response and reference are mathematically equivalent.
3. Analysis: error flagging, i.e. classifying the response’s individual elements into correct, missing, unrecognized, wrong, and redundant elements.

Parsers are widely used for matching purposes only (Phase 1). The RUReady parser design introduces three additional innovative ideas: (a) numerically evaluating both the reference and response expressions for both real and complex variable values to decide whether they are equivalent (Phase 2). This approach is simpler, more reliable and more general than computer symbolic algebra systems for the considered educational applications; it also allows a user-defined tolerance in comparing the expressions. Numerical evaluation to verify expression equivalence has been employed before, for example WIMS (Gang, 1999); however, the specific algorithm for choosing sample values and for testing numerical equivalence is new, and was also verified to be robust on a large set of student responses; (b) comparing the response syntax tree in relation to the specific reference syntax tree, rather than reducing both to absolute normal forms and comparing the normal forms; (c) generating meaningful error flagging (Phase 3), using Approximate Tree Pattern Matching (ATPM) (Shasha, 1997; Wang, Zhang, Jeong, & Shasha, 1994). The ATPM approach computes the edit distance, which is the minimum number of edit operations required to transform the response syntax tree to the reference syntax tree. A byproduct of the minimization algorithm is a nodal mapping, which pairs each response tree node with a reference tree node. Depending on the syntax and complexity of the expressions, some nodes may have no counterpart. Each response element (a number, operation, variable or function) is classified accordingly and highlighted as correct, missing, unrecognized, wrong, or redundant. For more details, see Livne, Livne, and Wight, (2006). An interactive parser demo is available online at http://ruready.net/demo, where a user can provide a reference string and a proposed student response string, and view images of the generated parser analysis and scoring. The parser is a powerful stand-alone tool to detect students’ errors, as well as the backbone of the overall RUReady learning and assessment system.

Automated Partial-Credit Scoring Model
Based on the parser’s error analysis, each student response is assigned a partial score on a continuous scale of 0-100, as recommended by the National Assessment Governing Board (2004). The score is a weighted sum of two components:

1.       Overall response correctness (right or wrong) determined by the numerical evaluation of the mathematical expression in Phase 2. The response and reference strings must be equal to within a user-defined tolerance (a 10^-3 relative tolerance is normally sufficient for educational applications). This component assumes a binary value a: a=1 if the response is equivalent to the reference and a=0 otherwise (see the first component in Figure 1).

2.       Fraction of correct elements, which is the number of correct response elements (C) divided by the total number of correct (C), missing (M), unrecognized (U), and wrong (W) elements (identified in Phase 3; redundant elements are not counted as errors. See the second component in Figure 1). 

          
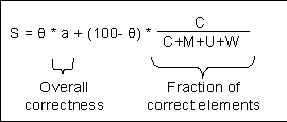
           Figure 1. The Parser Scoring Model defines the response
           score as a convex combination of the two components.

The precise weighting, 0 ≤ θ ≤ 100, of the two components was optimized in the validation study described below. The scoring formula was found to be generally applicable and robust for a large set of real-world constructed responses to questions in a college pre-Calculus course. It replaces current content-dependent rubrics, which require complicated development and parameter tuning for specific questions. The parser scoring model is described in detail in Livne, Livne, and Wight (2007b).

The same scoring algorithm can also provide partial scoring for MC questions: each choice is regarded as a prospective constructed response, so that partial-credit is also assigned to each distracter depending on the error types it contains. Furthermore, when designing a new question, a teacher can use the parser score in creating proposed distracters corresponding to common student misconceptions. Given that MC questions in all other assessments are scored as correct/incorrect (for example, see Villamide et al. 2006), the RUReady continuous scale provides a substantial improvement over the current multiple-choice testing framework (Livne et al., 2007b).

Results

Study 1: Can a Computer Closely Match Human Graders: External Validation of the Parser Scoring Model?

This study was designed to determine whether the parser model could closely match human partial-credit scoring, thereby externally validating its scoring algorithm. The parser scoring model was compared directly with human teacher grading, as recommended by literature (Bennett & Bejar, 1998).

To that end, three mathematicians, who were both University mathematics faculty and also teachers of college-level mathematics courses in high schools, were asked to independently score (on a scale of 0-100) a sample of 207 real-world mathematical constructed responses along with their matched questions. The responses were collected from high school and pre-college students that had worked through the RUReady site. In addition to the total score, the scorers also indicated the number of structural errors and the number of computational errors in each response. Because the number of different scored responses in this study was relatively large (N = 207), only three scorers were used. Notwithstanding, this meets the literature recommendation of three or more graders to ensure a reliable measure of scoring twenty or more responses (Seigel, & Castellan, 1988). To examine the degree of agreement among teachers on scoring the 207 responses, Kendall’s coefficient of concordance, which is considered the most appropriate measure for more than two scorers, was used (Gibbons, 1993; Seigel & Castellan, 1988). The results indicated that there was strong agreement among the three human graders on scoring each response; the overall Kendall’s coefficient of concordance (Kendall, 1948) was W = .890, p < .0001, regardless of the level of difficulty of the questions.                          

Stepwise linear regression was used to predict the human score by the two parser scoring model components. Interestingly, the fraction of correct elements explained 77.3% of the human scoring variance, whereas the overall correctness contributed only an additional 5.8%. The optimal weights of the two scoring components in Figure 1 were (by definition) their loading coefficients in the final regression (θ≈30, 100–θ≈70 for the overall correctness and fraction of correct elements, respectively); with these weights, the parser scoring model explained an impressive 83.1% (the sum of 77.3% and 5.8%) of the human scoring variance, which is equivalent to a human-parser score correlation coefficient of r = .910, p < .0001.  See Table 1. 
 

Table 1. Stepwise Regression Analysis of Predicting Human Teacher Scoring by the RUReady Parser Scoring Components

The concordance of the human and parser scoring scales was examined by the regression line slope. As illustrated in Figure 2, the slope was 0.97, indicating that a parser score of 100 corresponded to a human score of 97. Thus, the two scales almost coincided. Overall, the results indicated that the parser scoring model closely matched human scoring, ensuring that every student response in the RUReady site is automatically awarded accurate partial-credit, similar to what a human teacher does.

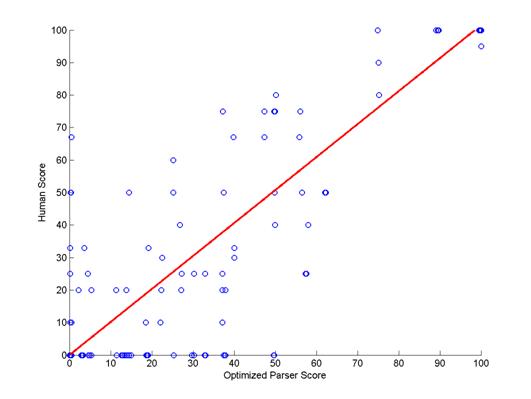
            Figure 2. Scatter-plot and regression line of RUReady parser scoring (horizontal axis)  versus
            human teacher scoring (vertical axis) of mathematical constructed responses.

To determine whether the parser scoring was a consistent measure, it was compared against the average and variation in human scoring. First, the standard deviation (SD) of the three teacher scores was computed for each of the 207 responses. Then, the difference (PD) between the parser score and the average teacher score was computed for each of these responses. The consistency of the two scoring methods (human and computer) was compared by means of a paired sample t-test on the difference between the mean SD and the mean PD. Because the correlation between the parser and human scorings was high, it was anticipated that the two scoring methods would be consistent.

As expected, the difference between the two means was not significant across all 207 responses (MSD = 9.923, SD = 12.291 and MPD = 10.583, SD = 15.045, t₍₂₀₆₎ = -.618, p = .537). This implied that the parser scoring algorithm matched human teacher scoring and exhibited equal consistency and reliability.

To illustrate the human-parser scoring match, consider the question:

“What is the point-slope equation of the line perpendicular to the line
2x - 9y = 22 and containing the point (27,-19)?”.

The correct answer is y + 19 = -(9/2)(x-27) ,whereas the student’s response was y + 19 = (2/9)(x-27). This response was scored 70, 67 and 50 by the three teachers, while the parser’s score was 55 (30 times the overall correctness (0) plus 70 times the fraction of correct elements, which was 0.786).

While the teacher mean score was 62.3 with a reerpendicular lines, albeit correctly using the point-slope formula. Based on this heuristic, a score around 50 (one correct concept out of two) would be expected. Nevertheless, each teacher penalized and scored the student’s response differently. This illustrates that the parser scoring was meaningful even when the score assignment was not clear-cut (either a totally wrong or a totally correct response), but lay in a “gray area” that required human expertise to award meaningful partial-credit.

Study 2: Can a Machine Surpass Human Teacher Scoring: Automatic Detection of Student’s Structural versus Computational Error Patterns?

Based on the validity and reliability of the parser scoring model described above, a second study was conducted to ascertain whether the different error types detected by the parser corresponded to different error patterns exhibited by students. Specifically, 124 additional real-world students’ constructed responses to pre-Calculus questions were analyzed and scored by the parser. To examine the internal structure of the error types and decide whether they could be clustered, exploratory factor analysis with a varimax rotation method was conducted (Hair, Anderson, Tatham, & Black, 1995). It yielded two distinct factors (error groups) that explained an impressive 76% of the original error elements’ joint variance: (1) Error Group 1 included the missing and unrecognized elements, with factor loadings of .768 and .822, respectively; (2) Error Group 2 included wrong elements only, with a factor loading of .986. Moreover, to examine whether the two Error Groups’ average frequencies were different, a paired sample t-test was used. The result indicated that the mean percentage of elements in Error Group 1 of the total number of response elements (20.242%) was significantly higher than that of Error Group 2 (10.747%) across all 124 responses (t₍₁₂₃₎ = -4.380, p < .0001). Cohen’s d, which is the appropriate effect size coefficient for a t-test (Cohen, 1988) was .661, indicating that the two Error Groups were indeed distinct for a relatively small response sample size (a value of d =.5 is considered a medium effect size; see Cohen, 1992). Taken together, these results indicated that two distinct types of errors were detected in students’ responses.

To further investigate whether the two error groups identified by the parser had different effects on predicting the score of students’ responses, stepwise linear regression was performed. The results indicated that missing and unrecognized elements combined (Error Group 1) explained 36% of the student score, representing structural errors that might reflect conceptual errors, while wrong elements (Error Group 2) contributed only 19%, representing computational errors that could also be a result of typographical errors. Taken together, the two error patterns explained 55% of the students’ scores, which was equivalent to an error-score correlation of r = .74, p < .0001. The correct parts explained 45% of the scores’ variance. These findings supported Orton’s (1983) results that Calculus responses of college students were classified into ‘structural’ versus ‘executive’/computational errors. Structural errors were those "which arose from some failure to appreciate the relationships involved in the problem or to grasp some principle essential to solution (Orton, 1983, p. 236)." In contrast, ‘executive’ errors involved failure to carry out computational manipulations, though the principles involved may have been understood (Orton, 1983). Moreover, our results were also in line with previous postulations that student error patterns generally fall under two categories: bugs and slips (Acton, Johnson, & Goldsmith, 1994, Ginsberg, 1987). Bugs represent systematic conceptual errors that are consistently made by a student and in our study could possibly correspond to Error Group 1. Slips represent minor deficiencies in applying the correct rules and techniques to the solution process that presumably correspond to Error Group 2.

To determine whether teachers used similar error detection heuristics to give partial-credit scores, stepwise regression was also conducted to predict human teacher scores using the structural and computational Error Groups. The results showed that Error Groups 1 and 2 explained 18% and 15% of the human scoring variance, respectively. Taken together, the two Error Groups explained 33% of the variance in the teacher scores, which corresponded to an error-score correlation of r = .58, p < .0001. These results lead to two assertions: (a) although the parser and teacher total scores concurred, teachers penalized students almost evenly on structural (account for 18% of their total score) and computational errors (15%); the parser penalized students twice as much on structural errors (36%) than on computational errors (19%); (b) teachers focused more on correct parts of students’ responses (67%) and less (33%) on students’ error patterns; in contrast, the parser gave similar weights to both the correct and erroneous parts of the student’s response (45% and 55%, respectively, as cited above). 

In particular, human graders ran into difficulties when asked explicitly to classify students’ errors into structural and computational error groups (patterns), similar to those generated by the parser. There was a very low agreement among the teachers on error classification, and each teacher came up with different error grouping (W = .106 and W = .021, p = .012 for the structural and computation error groups, respectively). Moreover, the correlation between the mean number of structural errors defined by the teachers and the sum of missing and unrecognized elements detected by the parser, was relatively low (r = .456, p < .0001); the corresponding correlation for the computational error group was not significant at all. The results indicated that human graders failed to establish a systematic heuristic to detect error patterns in students’ responses. In contrast, the parser provided a consistent mechanism to distinguish between the two main error types in students’ responses.

Discussion, Limitations, and Implications

The current article describes a novel parsing system that automatically scores students’ constructed responses to mathematics questions, based on the errors in each response. This computerized scoring provides a good match to human grader scoring, and goes beyond human graders in distinguishing between two types of error patterns: structural possibly reflecting conceptual errors  and computational possibly resulting from typographical errors.

The findings provide evidence that the parser generates partial-credit scores to constructed responses in mathematics that are very similar to human-generated scores. This indicates that the parser scoring model can replace human scoring, thus, positively answering the first research question posed in this article, viz., Can a computer closely match human graders? The machine scoring was at least as consistent as humans, owing to a uniform scoring formula as opposed to frequent inter-teacher scoring deviations. Furthermore, it generated automatic partial-credit scoring at a much higher speed than manual grading by humans. The authors anticipate that these advantages of the parser scoring will be more pronounced in a larger sample of human scorers as well as in larger response samples.

Furthermore, although the overall scores given by the parser and human graders were highly correlated, the results support the postulation that the parser can further unveil human scoring errors and distinguish between two main types of student error patterns, two areas in which human graders fall short. The value of engaging students in the analysis of their errors has long been recognized in computer programming, where students are expected to debug their incorrect programs (Melis, 2004). Similarly, the parser’s unique capability to generate error feedback by highlighting correct versus erroneous elements (i.e., incorrect, missing, unrecognized or redundant) for each response, stimulates students to figure out what went wrong, organize error patterns (Livshits & Zimmermann, 2005; Melis, 2004), and find their corrections (Babbit, 1990). Through analyzing their errors, students develop a deep understanding of why the answer was wrong and what the mathematical concepts behind it were, rather than focus on how the problem could be solved with a rule or formula (Melis, 2004, 2005; Oser & Hascher, 1997; Russell, 2007). Error feedback was found to be the most reliable mode to reduce common errors in mathematics and to increase students’ understanding and performance (Koedinger & Anderson, 1990; Larkin & Simon, 1987; Melis, 2004; Novick, 2001). In contrast, human graders often tend to largely avoid pointing out and grading individual error patterns; instead, they focus more on what the student knows, relying on the traditional yet disputable behaviorist view that errors could interfere with fixing the correct result in the student’s mind (Miller, 1983). Accordingly, it is concluded that the parser can surpass human grading in detecting errors patterns, as hypothesized in the second research question.

Overall, the answer to the title question is YES: Automated machine scoring can surpass hand-grading of constructed responses and error patterns in mathematics.

The RUReady parser is still limited to scoring only the final answer, as opposed to examining all of the intermediate steps. This limitation is particularly evident when the final answer is a number, which might nevertheless be a complex function of several intermediate stages that reflect back on errors made during the problem-solving process. Future plans call for parsing intermediate solution stages, as well as inferring on different types of errors made during the whole solution process. This will allow the detection of the sources of different error types, thereby identifying the conceptual versus computational or typographical errors. Moreover, creative open-ended problems that have multiple solution paths but only one final answer could then be employed (Becker & Shimada, 2005), revealing the level and the quality of student mathematical understanding (Magone, Cai, Silver, Wang,1994; Moon & Schulman, 1995). The authors also plan longitudinal studies to investigate the capability of the RUReady assessments to predict student success in specific college-level courses in mathematics.

Notwithstanding, the parser evidently illustrates that natural languages and artificial intelligence principles can be used successfully to detect student error patterns. Additionally, the RUReady parser offers several advantages over the limitations of multiple-choice questions in automated assessment tests. It provides automatic, immediate partial-credit scoring of computerized mathematical exams, which need not be hand-graded as with other systems. The exclusive use of questions that require constructed responses also fosters the development and measurement of creative problem-solving skills. The same technology enables the construction of online learning tools that generate immediate automated error feedback to guide student learning in real-time. It provides a tool for teachers to design concept-based instructional units tailored to student’s individual misconceptions. Further, it allows teachers to construct multiple-choice mathematical questions that are scored on a continuous scale, much like constructed responses. Future studies could explore the optimal distribution for MC continuous scores, as described in more details elsewhere. (Livne, et al., 2007b).

In conclusion, the RUReady parser constitutes an important tool to enhance college readiness in mathematics on a broad scale. By taking full advantage of the low cost per student of machine scoring, it is now feasible to construct automated online learning tools to help level the playing field for underrepresented student populations and promote diversity in science, mathematics and engineering disciplines.

References

Acton, W. H., Johnson, P. J. and Goldsmith, T. E. (1994). Structural Knowledge Assessment: Comparison of Referent Structures. Journal of Educational Psychology 86, 303-311.

Ashton, H. S., Beevers, C. E., Korabinski, A. A., & Youngson, M. A. (2006). Incorporating partial-credit in computer-aided assessment of mathematics in secondary education. British Journal of Educational Technology, 37(1), 93-119.

Babbitt, B. C. (1990). Error patterns in problem solving. Paper presented at the International Conference of the Council for Learning Disabilities. Austin, TX. ERIC #:ED338500. Retrieved April 25, 2007, from http://eric.ed.gov/ERICWebPortal/Home.portal?_nfpb=true&_pageLabel=RecordDetails&ERICExtSe
arch_SearchValue_0=ED338500&ERICExtSearch_SearchType_0=eric_accno&objectId=0900000b8004e2b2

Becker, J.P., & Shimada, S. (2005). The open-ended approach: A new proposal for teaching mathematics. Reston, VA: National Council of Teachers of Mathematics.

Babbitt, B. C. (1990). Error patterns in problem solving. Speeches/Meeting Papers. ERIC: ED338500. Retrieved April 25, 2007, from http://eric.ed.gov/ERICWebPortal/Home.portal?_nfpb=true&_pageLabel=RecordDetails&ERICExtSe
arch_SearchValue_0=ED338500&ERICExtSearch_SearchType_0=eric_accno&objectId=0900000b8004e2b2

Beevers, C., & Paterson, J. (2002). Assessment in mathematics. In P. Kahn, & J. Kyle, (Eds.), Mathematics and its applications (pp. 51-53). Sterling, VA.: Stylus Publishing Inc.

Bennett, R. E., & Bejar, I. I. (1998). Validity and automated scoring: It‘s not only the scoring. Educational Measurement: Issues and Practice, 17(4), 12-17.

Bennett, R. E., Steffen, M., Singley, M. K., Morley, M., & Jacquemin, D. (1997). Evaluating an automatically scorable, open-ended response type for measuring mathematical reasoning in computer-adaptive tests. Journal of Educational Measurement, 34(2), 162-176.

CNN Online (3/28/07). Testing companies struggle to meet NCLB demands. Retrieved May 2, 2007, from: http://www.cnn.com/2007/EDUCATION/03/25/nclb.standardized.test.ap/index.HTML

Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2^nd ed.). Hillsdale, NJ: Erlbaum.

Cohen, J. (1992). A power primer. Psychological Bulletin, 112(1), 155-159.

Educational Testing Service (1997). The PRAXIS Series^TM. The PRAXIS Series, Educational Testing Service, Inc. Retrieved February 1, 2007, from http://www.ets.org/portal/site/ets/menuitem.fab2360b1645a1de9b3a0779f1751509/?vgnextoid=48c0
5ee3d74f4010VgnVCM10000022f95190RCRD

Gang, X. (1999). WIMS: A server for interactive mathematics on the internet. Retrived, August 25, 0.0pt;font-family:Arial">Gibbons, J. D. (1993). Nonparametric measures of association. Sage University Paper series on Quantitative Applications in the Social Sciences, 07-091. Newbury Park, CA:Sage.

Ginsburg, H. P. (1987). How to assess number facts, calculation, and understanding. In D. D. Hammill (Ed.), Assessing the abilities and instructional needs of students (pp. 483-503). Austin, TX: PRO-ED.

Hair, J. F., Jr., Anderson, R. E., Tatham, R. L.,& Black,W. C. (1995). Multivariate data analysis with reading (4^th ed.). Upper Saddle River, NJ: Prentice Hall.

Jarrett, D. (2000). Open-ended problem solving: Weaving a web of ideas. The Northwest Regional Educational Laboratory's Mathematics and Science Education Center (Volume 1 Number 1). Retrieved August 23, 2007, from http://www.nwrel.org/msec/images/nwteacher/spring2000/open.pdf

Kendall, M. G. (1948). Ranking correlation methods. London: Griffin.

Koedinger, K. R., & Anderson, J. R. (1990). Abstract planning and perceptual chunks: Elements of expertise in geometry. Cognitive Science, 14, 511-550.

Miller, P.H. (1983). Theories of developmental psychology. San Francisco, CA: Freeman.

National Assessment Governing Board. (2004). Mathematical framework for the NAEP assessment 2005.
 U.S. Washington, D.C.: U.S. Department of Education National Assessment of Educational Progress.

Novick, L. R. (2001). Spatial diagrams: Key instruments in the toolbox for thought. In D. L. Medin (Ed.), The psychology of learning and motivation (Vol. 40, pp. 279-325). San Diego, CA: Academic Press.