Introduction

Completion of an introductory mathematics course is usually a requirement in a wide range of postsecondary programs in the sciences (such as chemistry and computer science), social sciences (such as psychology and economics), and professional programs (such as business and engineering). 

This situation presents special challenges for teaching introductory and service courses, as these courses attract a wide range of students. In a first-year calculus course, for instance, students may range from mathematics majors to those seeking a single mathematics elective. As a result, the background and motivation of students taking the course vary considerably, making it challenging for a course to meet the needs of all students. On the one hand, students with weak mathematical backgrounds might not receive enough practice and become frustrated with material seeming to pose an unrealistic challenge to them, potentially even dropping the course. On the other hand, stronger students might not be pushed enough to realize their full potential. The only feedback that top students would receive is a perfect (or nearly perfect) score on all their assignments and tests. Even though they pay the same tuition as weaker students, and are in a sense an equal partner in the process, they may not receive much constructive feedback.

Larger institutions often attempt to solve this problem by streaming students into a range of introductory classes, although a wide range of abilities is usually represented in each class nonetheless. This approach is not practical at smaller institutions because of limited enrollment.

The above problems are often compounded by the fact that, according to surveys, about 85% of first-year students may feel some anxiety towards mathematics (Perry, 2004). “Math anxiety” is a well-known fundamental impediment to learning in post-secondary mathematics (Tobias, 1990).

Part of the solution to overcoming these challenges may lie in the use of an online interactive and adaptive learning environment that allows students to work on a series of computer exercises. As they progress, the software assesses each answer and provides the student with instant feedback as well as setting the difficulty of the next exercise based on the response.

Adaptive technology is well established in testing. In fact, most major computer-based standardized tests are adaptive in nature. For instance, the Educational Testing Service (ETS) offers computer-based adaptive tests, such as GRE, GMAT and TOEFL. Private certifications, such as those offered by Microsoft and Oracle, also use these methods to deliver more effective testing. The primary advantage of computerized adaptive testing is that a much finer distinction of ability can usually be made in a shorter timeframe than with traditional testing. For example, a twenty-question True/False test would traditionally provide only one of twenty-one possible grades from 0 to 20. However, in a twenty-question adaptive test the next question asked could depend on all the previous answers, thus doubling the number of possible distinct tests at each step. Accordingly, if two students start with the same initial question, they may each potentially write one of 2¹⁹=524,288 distinct tests. In a non-True/False test, an even larger number of distinct tests is possible if incorrect answers are sub-classified.

The focus of this article is on creating interactive and adaptive assignments. Nonetheless, it is believed that benefits similar to those of adaptive testing can be derived from using adaptive technology as a teaching tool incorporated into practice exercises and assignments. The traditional approach to adaptive testing has been to create a large bank of multiple-choice questions as well as a method for classifying the student's level, and adjusting successive questions accordingly.

There are many well-known pedagogical arguments against using multiple choice questions, ranging from not wanting students to work backwards from the answers to wishing to avoid increased measurement error due to random guessing that could make branching decisions in adaptive testing problematic (Bridgeman, 1992).  Furthermore, producing large banks of questions and solutions can be resource-intensive, especially in the sciences, where questions and solutions often require non-textual information such as complex notations, equations and diagrams. In quantitative science courses, however, it is often possible to create algorithmically generated questions. In calculus, for example, a student could be presented with a random polynomial to differentiate, while in chemistry a student could be provided with a chemical equation with random coefficients to balance. In these cases, the student's answer could be compared for correctness against a general solution for that type of problem. A virtually unlimited number of similar questions could be produced from a single template. Note that, if the underlying software is powerful enough, it is not necessary to rely on multiple choice responses.

Having a virtually unlimited choice of possible questions could make it possible to create adaptive assignments. The following are examples of how an assignment could be made adaptive:

·      Changing the parameters in a template to make questions more challenging as a student improves. For example, a general polynomial factoring question could evolve from factoring quadratics to factoring cubics.

·      In a multi-step question, the number of steps to assist the learners could decrease as they improve.

·      The size of the pool of templates could increase drawing material randomly from a larger portion of the course. The rate at which new questions are introduced and reviewed could be adapted to an individual's learning curve using artificial intelligence algorithms.

Technology

An open-source (under a GNU Public License) adaptive learning platform called Xero is being developed and is expected to be available in the fall of 2007. It supports the aforementioned adaptive models, using Bayesian learning and neural network algorithms to aid with parameter selection.

Currently there are no robust open-source software packages for adaptive mathematics. While it is possible to create simple interactive parameterized questions in a number of platforms, such as WebCT/Blackboard, there are two general-purpose open-source interactive environments: WeBWorK (see Hauk and Segalla, 2005) and WIMS (Xiao, 2001;  Khaznadar, 2005) which can create fairly complex mathematics questions. WIMS is the more powerful of the two environments, and Xero is derived from WIMS. WIMS has been reviewed in MERLOT's Learning Materials Collection, and several individual WIMS activities have also been individually reviewed. With a few changes, WIMS materials can be imported into Xero.

Xero provides much of the functionality of a course management system: announcements, file management, chat rooms, message boards, and functionality for online tests, quizzes and assignments.   However, the main focus of Xero is providing a facility to create adaptive template-based exercises and an environment for adaptive online assignments. The Xero server interfaces with many well-known open-source mathematics software packages. For example, the server uses, among others, computer algebra systems such as Maxima (comparable to Maple) and Pari-GP for symbolic calculations, the TeX mathematical typesetting system for displaying mathematics, and Gnuplot to create 2D/3D plots. 

For example, a random function could be generated (say a*x^b*e^cx+d+ same function. A single general function with enough terms could represent virtually any function thstudent could be asked to differentiate in an introductory calculus course. For example, in the above function, letting c=d=0 and b=2 would provide a general quadratic function, while a=1, b=f=g=0 would produce a general exponential function with linear power.

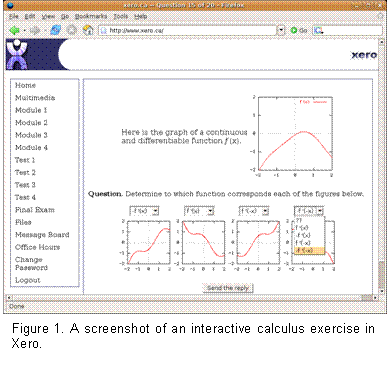Graphical questions could also be parameterized. For example, the exercise depicted in Figure 1 is a Xero exercise that has been converted from the Graphical Derivatives WIMS exercise reviewed by MERLOT. In this exercise, a random function is drawn, along with a number of functions related to its derivative. Students are asked to identify the relationship between the functions. Each time students answer the question, they are presented with the correct associations. This exercise can be very effective in developing the intuition of calculus students in service courses, especially when they practice with a large number of these examples. What follows is an example drawn from a mathematics service course for computer science students.

Example of Challenges in Teaching a Mathematics Service Course for Computer Science Students

Computer Science students are often required to take several mathematics courses, such as calculus and discrete mathematics (which usually includes counting techniques). The question, “How many ways can the letters of ABRACADABRA be rearranged?” is a standard discrete mathematics example that serves as a counting model. The importance of this example was emphasized in lectures, as it emphasizes valuable counting techniques, and several questions with different words to rearrange or objects in place of letters were assigned as homework. Then, the question “How many ways can 11 identical jelly beans (5 Red, 2 Black, 2 Purple, 1 Orange, 1 Green), be arranged in a row?” was placed on a test. Only about 20% of the students were able to answer it correctly, even though it is identical to the above question, with letters replaced with colored jelly beans. In general, it appears that students in the course did not internalize the above counting model.

This indicates that it may be necessary to assign more questions of each type. There are, however, a large number of counting techniques that must be learned in a discrete mathematics course, and it is not possible to provide more than a few questions of each type on a typical assignment due to limited marking resources as well as concerns about assigning too much work to students in a service course. Experience suggests that the reaction of students can vary depending on whether the course is for mathematics majors or for other students. In courses taught to mathematics majors, when workload or difficulty increases, students often exert more effort and grades remain mostly unchanged. In service mathematics courses, however, greatly increasing workload or difficulty tends to result in a combination of poor retention and decreased grades. The anxiety that many students have towards mathematics may be affecting their motivation. To attempt to solve this problem, computer-assisted assignments were explored.

Implementation of Online Assignments

Online assignments were implemented in two service courses: a first-year applied calculus course with 20 students, which was taught completely online and restricted to non-mathematics majors; and a traditional second-year discrete mathematics course with 44 students, which was taught primarily to computer science majors.

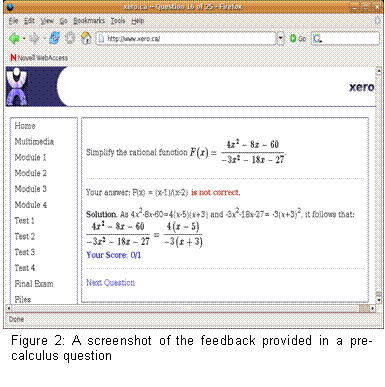In the calculus course, all assignments and tests, as well as the final exam were online and used the Xero technology mentioned above. In the discrete mathematics course, online and paper assignments were alternated such that the second and fourth of five assignments were online. The material covered on the assignments had significant overlap, since some topics, such as techniques of proof, make poor online assignments as their grading needs to be subject to human judgment, while many quantitative topics require repeated practice and so make better online assignments. An anonymous paper survey was administered in class following each online assignment in the discrete mathematics class. Surveys were not conducted in the calculus course, due to logistical and other challenges involved in creating an anonymous online survey. Hence, the results that follow are primarily from the discrete mathematics class, but are, nonetheless, consistent with the results from the calculus class.

In the first discrete mathematics assignment, questions were grouped in three groups of ten under the topic headings: logic, sets and functions, and sequences and series. Each time a set of questions was attempted, a randomized series of questions were generated. Students were required to answer the questions in order. Each time a question was answered, a solution or answer was immediately displayed before the next question was attempted (see Figure 2). After each set of 10 questions was completed, students would be able to reattempt the set as many times as they wished with new randomized versions in order to improve their grade. In order to provide more motivation to practice, the best grade was the one that was kept. The second assignment contained two sets of questions, one with 15 questions from combinatorial counting and the other with 10 questions from probability.

There was one major difference between the assignments. The first assignment consisted mainly of questions for which there were no examples in the lectures or the textbook. The assignment was designed to be a learning tool for students to learn new material. However, in the second assignment a different approach was attempted. Questions were chosen to reinforce concepts taught in the lectures and book. In each case, students had two weeks to complete the assignment, the same as for a paper assignment. A typical paper assignment had 15 questions, some with multiple parts. Accordingly, a paper assignment might effectively have the equivalent of 25-30 online questions.

Below is an example of possible questions that can be generated from a template for a counting problem:

How many ways can 10 {distinct | identical} {books | containers | jars} be placed {in | on} 5 {labeled | unlabeled} {boxes | shelves} if the order that the objects are placed {in the boxes | on the shelf} {matters | does not matter} such that any {box | shelf} can have {any number of | at most 4 | at least 2} {books | containers | jars}.

In this case, integers in bold were randomly selected, and in each presentation only one word/phrase from every bracketed set was selected. For each attempt at a set of counting problems, 15 templates were selected from 33, and presented in a random order. All templates could produce a variety of different possible questions. For students, this created the impression of there being an almost unlimited number of different possible questions. A common comment on student surveys, as expressed by one student (student's emphasis) was a follows:  “I don't think I EVER got the same question twice.”

As online assignment questions for each student were randomly generated, students were allowed to discuss possible solutions to problems with each other. To further encourage students, a message board was set up that allowed for communication using mathematical symbols, and bonus marks (ranging from 1 to 4 percent of the assignment value) were awarded to the most active participants. Online office hours were also held regularly using a mathematical whiteboard program called enVision (Pollanen, 2006; Hooper, Pollanen & Teismann, 2006), in which students were allowed to participate anonymously. 

Learning Outcomes

Traditional paper assignments usually serve a dual role: as a learning tool, and as an assessment tool. By allowing an unlimited number of attempts for the online assignments, the emphasis is shifted towards their serving as a learning tool. The primary method of determining the effectiveness of the approach was student surveys. One was conducted after each of the online assignments in the discrete mathematics course.

Survey Results:

In Table 1 (below), we summarize the quantitative results from each of the surveys. The data on the amount of time spent and number of questions answered is from student estimates. The average number of questions answered on assignment #2, as estimated from the group of students participating in the survey, is 265. This is relatively close to the 252 questions per student for the entire class, as estimated from Web-server logs.  It is also interesting to consider the assignment averages. The assignment average for all assignments in the previous year was 72.1%, while the averages on the first and second online assignments were respectively 78.9 and 72.0%.

Table 1: Summary of quantitative results from surveys conducted after assignments #2 and #4

The surveys also allowed students to provide qualitative feedback, the results of which support the quantitative results. It would appear that online assignments were well liked, as backed up by qualitative comments from the survey:

“I love online assignments.”

“I really enjoyed this format.”

Although students thought they were difficult:

“Crazy hard questions... very good way of doing an assignment.”

“It was time consuming but I didn't mind.”

“Assignment #2 was challenging but helpful to see the right answers right there.”

An important aspect of this seems to be that the solutions were presented immediately, which aided in learning:

“Got immediate feedback, which corrected some of my misunderstandings.”

“It told me right away if I was wrong and gave me the right answers. Then I could figure out where I went wrong and not make the same mistake next time.”

“In a lot of cases something which I thought I knew 100% ended up being partly wrong. Thus I caught it.”

“I was able to improve right away rather than wait a couple of weeks.”

Overall, most students indicated that they learned more from the online format:

“All assignments should be online because we learn more and the tests could be made a bit more difficult to compensate.”

“I found I took more away from [the online assignment].”

“It really challenged what I thought I knew well.”

It appears from student comments that students were very motivated to work on online assignments, compared to regular paper assignments. This will now be analyzed from the standpoint of Keller's ARCS Model of Motivation.

ARCS Model of Motivation

During the 1980s Keller (see Driscoll, 1993 for a review) in a series of papers (Keller, 1983; Keller, 1984) developed the influential ARCS Model of Motivation for instructional design. ARCS stands for Attention, Relevance, Confidence, and Satisfaction, and represents a set of conditions which must be met for a learner to be motivated to learn.

Attention: In order to motivate students to learn, you must gain and keep the learner's attention.

As demonstrated above, most students enjoyed the online format more than paper assignments, which is an important factor in keeping their attention. Keller suggests that varying the presentation and providing visual stimuli is important as well, something that students mentioned:

“I appreciated the visual aspect of the assignment, the chance to see the solutions. The slight variations of questions on each turn means that you have to understand how the question is done. Plus, I found the online aspect quite enjoyable.”

A large number of students indicated that the assignment was entertaining or had “game-like” qualities:

“In an odd way it was more fun and entertaining.”

“Fun, learned immediately if I was doing things wrong. This made it like a challenging game.”

A considerable amount of research (see Randel, Wetzel, and Whitehill, 1992) has been conducted regarding the positive impact that games can have on learning. While they may be effective in maintaining attention, they can have significant drawbacks: complex educational games are often expensive to develop and can be time consuming to use. It still remains difficult at this time to see how they can replace a substantial portion of any advanced mathematics course, where multiple and diverse topics can be covered by an instructor in any week. It is interesting to see, though, that these online assignments can act as valuable supplements to traditional teaching and learning approaches by changing the way that traditional assignment questions are delivered to students; it appears possible to maintain a high density of learning with low development costs, and yet foster the motivation associated with an atmosphere of game-like learning.

Relevance: In order to motivate students, it is important to make the material relevant to the learner. 

The number of topics that are required to be incorporated into mathematics service courses, and the wide range of student backgrounds often make it challenging to incorporate many applications in these introductory courses. Furthermore, students often find applications frustrating until they have mastered the basic underlying skills.

It is therefore necessary to consider the relevance of assignments from a short-term point of view. Does the online assignment help a student meet their immediate objective of doing well in the course? This is not an easy question to answer as – although decades of research have been conducted – the role of assignments and homework on achievement still remains unclear (Trautwein and Köller, 2003).

In order to increase immediate relevance, the concept of an “open test” was attempted for the second online discrete mathematics assignment: all the questions had the same wording and form as questions that students had practiced with. This made the learning objective quite transparent. It was announced when the assignment was assigned that the next test would consist of tons changed. Although the problems on the first section of the test were substantially more difficult than the test problems from the previous year, students performed much better. On the second part of the test, students performed about the same as students in the previous year.

Even without an open test, it can be argued that online assignments are better for preparing students for a test. In a textbook, questions are already categorized by subject and technique, so approaches to questions can often be guessed at based on the section of the textbook they are found in. Furthermore, the questions in each section are often arranged in order of difficulty or type. However, on a test, any particular question may come from one of many sections, and the difficulty cannot always be guessed in advance; an online assignment can be much closer to a test situation.

Confidence: To motivate students, they must gain confidence from the activity.

One concern with the online assignments was that, as questions were substantially more difficult than for regular assignments, most students did poorly on their first attempt. See Table 2 below for the average scores for the first five attempts.  These scores are typical of what we saw in the other online assignments in both the calculus and discrete mathematics courses. 

Table 2: Average score on each of the first five attempts of the second online assignment

This gave rise to the concern that the assignment would negatively affect student confidence. To address this concern, on the second survey a question was asked regarding the effect of assignments on confidence. Of the 23 students who answered the survey, 22 indicated that the assignment had a net positive effect on their level of confidence. Only one student indicated that it had a negative effect on confidence. Some comments from students were as follows:

“At first it seemed really tough, but I took my time and got help (which is something I don't normally do) and it worked out fine. I think overall it had a positive effect.”

“When I did badly the first time it motivated me to do better and try harder the next time.”

“[It built] confidence over time.”

An important factor in managing confidence is communication. Many students mentioned that the message board was very useful, and reports regarding the class average on the assignment were helpful:

“Definitely motivated me, especially when I heard that I wasn't the only one struggling.”

Many students also mentioned that despite initially performing poorly, the fact that they saw their score improving provided them with an effective measure of how much they were learning, and motivated them further. It is interesting to note that students using a significantly above average number of attempts were generally weaker students in the course, however, relative to the other students, they typically ended up doing much better on the online assignment than on the paper assignments

Satisfaction:  To motivate students, the learner must be satisfied with the outcome.

One way for students to be satisfied is if they feel that they have ownership over the learning process. This may take the form of reaching their desired score:

“It caused me to keep working until I got a mark that I was happy with.”

“The low grade the first few times makes me work harder to get a better one.”

Some feel that they gain a sense of independence:

“We can realize our mistakes and [correct] our errors without [the professor’s] help.”

Others believe that they gain a deeper understanding:

“I can try different questions of the same type. It helps me to understand what the question is about... like the essentials of a problem.”

Discussion & Future Research

The concept of “unlimited attempts” for online assignments and quizzes is not new. This functionality exists in course management systems like WebCT and interactive mathematics platforms such as WeBWorK, and is usually accomplished in one of two ways. One way is to allow students to repeat an entire assignment (which is usually multiple choice with limited randomization) after viewing their score, without telling them which questions they answered incorrectly. Another method (Hauk and Segalla, 2005) is to allow students to repeat, without seeing the solution at each step, an individual question until they are successful. This is the first study that examines the impact of allowing students to repeat highly randomized template-driven assignments that provide solutions or answers after every question.

The long-term goal of the Xero project is to create an adaptive learning environment that can create an individualized learning experience by fitting assignments to personal learning curves and motivational profiles. The method of allowing students to repeat the assignment an unlimited number of times can be viewed as a very elementary form of adaptivity in that students requiring more practice generally take more attempts than stronger students.

A few of the question templates were designed to present problems with multiple steps. These were consistently the least favorite for students, though few students gave reasons. Perhaps these sorts of questions lose the “game-like” qualities. This might present a problem in creating adaptive assignments using a multi-step adaptive model, even though pedagogically it seems like a good idea.

Another challenge in moving to fully-adaptive assignments involves student perceptions regarding fairness. In our assignments, students were made aware of the method in which questions were generated. However, how will a student react to having assignments with different numbers of questions and questions of different difficulties than other students that are generated by complex artificial intelligence algorithms, even when the goal is to bring them to the same level as other students at the end of the assignment? Even in this experiment, one student commented that: “Some people seemed to have easier questions. Probably just lucky, but slightly unfair.” As a result of the large number of questions answered by each student, from the law of large numbers in statistics, it can be seen that the expected deviations in grades as a result of randomization should be insignificant. Perceptions can, however, often be more important than reality.

One interesting perception that students had was about the academic integrity of the assignment. Many students commented that they thought it would be difficult to cheat on the online assignments, as one student wrote: “I also don't know how you could possibly cheat? – Can't share answers with others.” Many studies suggest that academic dishonesty is rampant in universities (Lambert, Hogan and Barton, 2003). However, most students seemed to think there was less cheating on the online assignments. This suggests that a lot of cheating on assignments may be casual: it is easy to share answers on a paper assignment, but much more difficult to have somebody else complete an online assignment for you. Also, using “open testing” might remove some of the incentive to cheat. However, in discussions with other faculty, it seems that many faculty distrust the integrity of online assignments. This gap in perceptions between students and faculty would be worth considering further.

It is interesting to note that the student retention rate in the discrete mathematic course improved from 81% to 91%, although it is difficult to draw a conclusion from this. It is also noteworthy to consider that about half of the students in the bottom 25% of the class, the portion that might be considered “at risk”, performed extremely well on the online assignment by attempting it an above average number of times. Perhaps these students have poor mathematical skills and this assignment format allowed them to get the practice they needed. However, the other half of these at-risk students did extremely poorly on the online assignment. From logs it can be seen that they spent very little time on the assignment, although some of them mentioned to the instructor that they had worked very hard. Perhaps these students do not realize how much effort other students are spending on the assignment, or are unable to accurately gauge their own effort. It might be useful to provide each user with a log of the amount of time they have spent on the assignment, as well as an average for the class, to see if this motivates students to work harder.

Summary and Conclusions

In this paper a model for online assignments in mathematics service courses was presented. In the model students are presented with highly randomized template-driven assignments as well as solutions or answers at each step. The average difficulty level of the questions is chosen to be much greater than that for a paper assignment, but students are provided with an unlimited number of attempts, as well as discussion boards and incentives to discuss difficulties.

It is shown that students reacted positively to this model and ended up answering 7-9 times more questions than for a paper assignment of similar length. It is also shown that this model is consistent with the ARCS Model for Motivation, and results in a number of positive learning outcomes. 

References

Bridgeman, B. (1992). A Comparison of Quantitative Questions in Open-Ended and Multiple-Choice Formats. Journal of Educational Measurement, 29 (3), 253-271.

Driscoll, M.P. (2005). Psychology of Learning for Instruction (3rd ed.). Boston: Allyn and Bacon.

Hauk, S. & Segalla, A. (2005). Student perceptions of the web-based homework program WeBWork in moderate enrollment college algebra classes. Journal of Computers in Mathematics and Science Teaching,  24 (3),  229-253.

Hooper, J., Pollanen, M., & Teismann, H. Effective online office hours in the mathematical sciences, Journal of Online Learning and Teaching, 2 (3), 187-194.

Keller, J.M. (1983). Motivational design in instruction. In C.M. Reigeluth (Ed.), Instructional-design theories and models. Hillsdale, NJ: Erlbaum.

Keller, J.M. (1984). Use of the ARCS model of motivation in teacher training. In K.E. Shaw (Ed.), Aspects of educational technology XVII: Staff development and career updating. New York: Nichols.

Khaznadar, G. (2005). A server for education. Free Software Magazine, 4, 1-7.

Lambert, E., Hogan, N.L., & Barton, S.M. (2003). Collegiate Academic Dishonesty Revisited: What Have They Done, How Often Have They Done It, Who Does It, And Why Did They Do It? Electronic Journal of Sociology, 7 (4), online.

Perry, A. P. (2004). Decreasing math anxiety in college students. College Student Journal, 38 (2), 321-324.

Pollanen, M. (2006). Interactive Web-based mathematics communication, Journal of Online Mathematics and its Applications, 6 (4), online.

Randel, J.M., Morris, B.A., Wetzel, D.C., & Whitehill, B. (1992). The effectiveness of games for educational purposes: a review of recent literature, Simulation and Gaming, 23 (3), 261-276.

Tobias, S. (1990). Math anxiety: An update. NACADA Journal, 10 (1), 47-50.

Trautwein, U. & Köller, O. (2003). The relationship between homework and achievement – still much of a mystery, Educational Psychology Review, 15 (2), 115-145.

Xiao, G. (2001). WIMS: An Interactive Mathematics Server, Journal of Online Mathematics and its Applications, 1 (1), online.